Yeast: Millions Working to Get You Drunk

Beer would just be funky bread-water if not for yeast, but not all yeast is created the same. Brewer's yeast (also baker's yeast) is Saccharomyces cervisiae. Brewer's yeast is a facultative anaerobe, so it can respire aerobically (using oxygen) and anaerobically (without oxygen), but only anaerobic respiration produces alcohol. Aerobic respiration produces by-products that flavor the beer. Yeast prefers aerobic respiration and will ruin a brew if given the chance, but we need some aerobic respiration (thus oxygen in the wort) or the yeast won't reproduce enough.

Scanning electron microscope image of brewer's yeast.
Saccharomyces cerevisiae, Murtey and Ramasamy

Yeast contributes half the flavor (and all of the alcohol) of beer by fermenting different sugars to different degrees and producing small amounts of by-products.


Yeast population dynamics are of special importance to brewers. Too much yeast is expensive, but too little yeast makes brewing take longer, increases the amount of by-products in the beer, and can even result in a weak, sweet beer if there's not enough yeast to produce sufficient alcohol. The maximum fermentation density of yeast is 1.0 x 108 cells/millilter but to start with that much yeast in a 6 gallon (22,712.5 milliliter) wort would require almost 9 pounds (or 568 7g sachets as each sachet contains 4.0 x 109 cells) of dry yeast.

  6 gallons * 3785.41 mL/gallons = 22712.5 mL of wort
  22712.5 mL * 1.0 x 108 cells/mL = 2.27125 x 1012 yeast cells
  2.27125 x 1012 cells / 4.0 x 109 cells/sachet = 567.8125 yeast sachets (but we cannot easily have partial sachets)
  568 sachets * 7 g/sachet = 3976 g of yeast
  3976 g * 0.0022046 lbs/g = 8.7654896 lbs of yeast

Fortunately, science can help us determine exactly how much yeast we need to produce a good beer without breaking the bank.

Graph of yeast population curves with two different pitching rates.
Yeast Population Density, "Figure 3.4", p.88, Denny

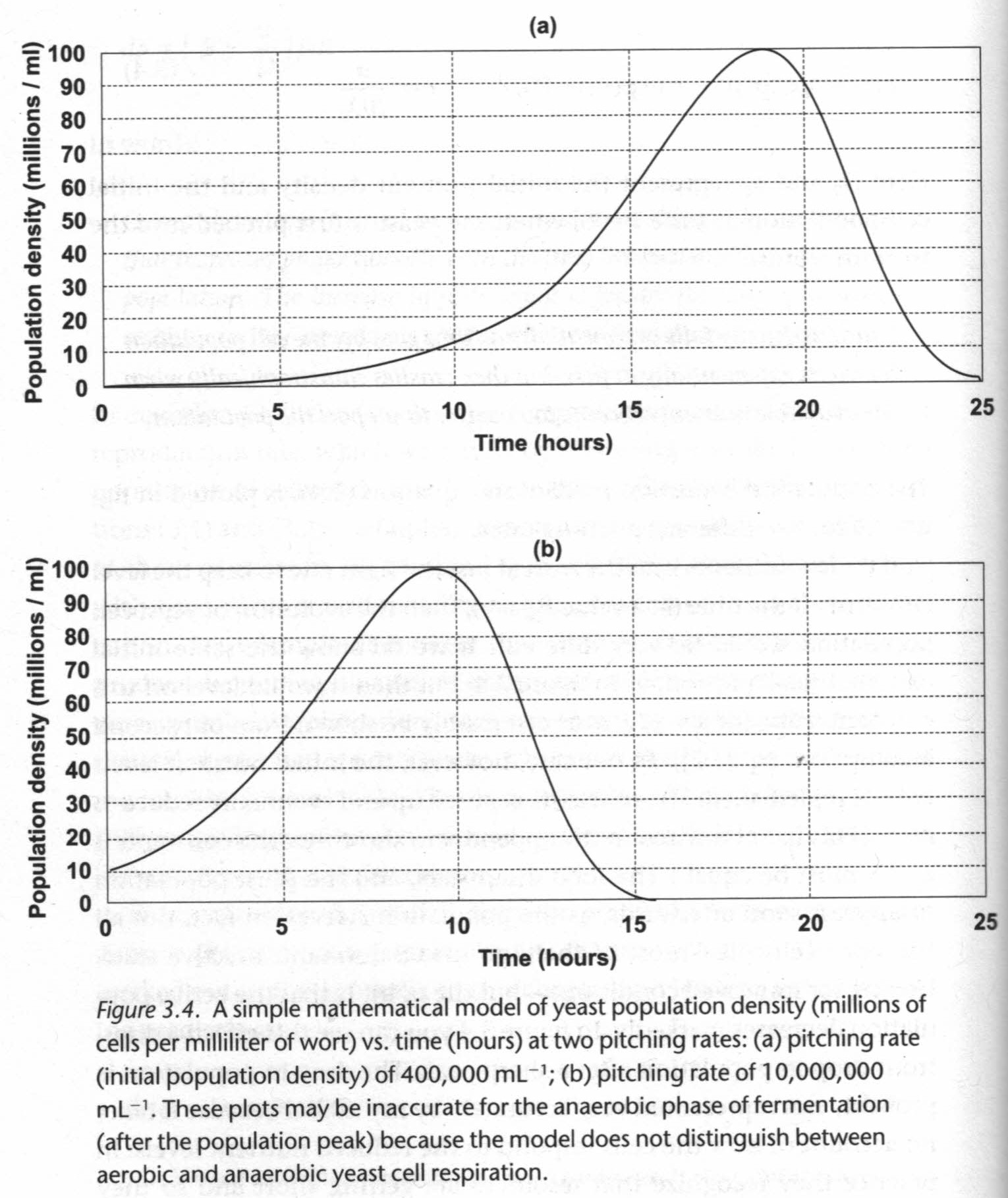
Yeast can double in population every two hours under ideal conditions, and brewers strive to provide those conditions so we'll use that for our calculations. Expert opinion is that the ideal yeast density for pitching is 10,000,000 cells per mililitter of wort. This pitch rate means the yeast will hit maximum fermentation density in only three to four generations.

  1.0 x 107 cells/mL * 23 generations = 8.0 x 107 cells/mL <
  1.0 x 108 cells/mL <
  1.6 x 108 cells/mL = 1.0 x 107 cells/mL * 24 generations

The figure to the left depicts the population curves for "typical" and "ideal" pitching rates.

If we only use two sachets of dry yeast, it will take an additional four to five generations (and eight to ten hours) to catch up.

  2 sachets x 4.0 x 109 cells/sachet = 8.0 x 109 yeast cells
  8.0 x 109 yeast cells / 22712.5 mL = 352228.9488 cells/mL of wort (but we cannot have partial cells)
  352228 cells/mL * 24 generations = 5.635648 x 106 cells/mL <
  1.0 x 107 cells/mL <
  35228 cells/mL * 25 generations = 1.1271296 x 107 cells/mL

This is one reason to reuse the yeast from a previous brew. There will be far more live yeast than we could obtain from sachets (without purchasing an exorbitant amount of dry yeast), and that yeast will have already adapted to our brew. Unfortunately, we can only do this for a few generations before the yeast mutates or there is too much risk of contamination.

Mathematics is the language of the physics, so we should be translate our natural observations about brewing into mathematics. First, some definitions:

  • Population, p = the number of yeast cells that are not dead or dormant
  • Food, F = nutrients and oxygen
  • Density of nutrients, D = F/p is the supply of food and oxygen available to each cell
  • Constant of proportionality, γ
  • Yeast fecundity (reproductive rate), β = 1/2 ln(2) = 0.35/hour
  • Yeast die-off rate, α

We know that, over time, the nutrient supply in our brew will decrease and that it will decrease faster the more yeast cells there are. A formal statement might be, "Over a short time interval, the nutrient supply falls by an amount that increases proportionally with the time interval and with the yeast population" (Denny, p.85). We can now easily say this in in physics:

  dF = -γp dt

That's not all. We know that yeast cell populations increase with their reproductive rate, that it decreases as there is less food per cell, that it changes over time, and that it changes faster (both positively and negatively) for larger populations. Formally, "Over a short time interval the yeast population changes by an amount that increases proportionally with the time interval and with the yeast population. The increase in population is greater for fast-reproducing strains, and the decrease is greater when the food density is low," in physics (Denny p. 86). The mathematics is a much shorter statement:

  dp = (β - α/D)p dt

There is more we can say about wort and the yeast that it contains. Such as, "Nutrient density falls exponentially as time goes by," and, "The cell population increases exponentially at first, but then crashes catastrophically when teh available nutrients become too meager to support the population" (Denny, p.87):

  • Wort nutrient density, D(t) = d0-βt
  • Pitching rate to peak density, r = α/βD0
  • Population at a specific moment of time, p(t), = p0βt - rβt - 1

This is a lot of math, but it shows how we can describe what we see, what we experience, what we attribute to "common sense" in "the language of physics". This allows us to not only describe reality but predict it: We can calculate exactly how much yeast we need for a given batch of beer instead of simply guessing.