Thermodynamics

Much of brewing depends upon managing heat: The grain and water are heated to mashing temperature, and then the mash must be held at that temperature for the enzymes to do their job. Too low of a temperature makes the enzymes sluggish while too high of a temperature destroys them. Even within the acceptable range, higher temperatures will eventually result in more alcohol and more body with the same grain and yeast.

After mashing, the wort is boiled to prepare it for the yeast. Then the hot wort must be cooled to a yeast-friendly temperature, and then it must be kept at this temperature throughout primary fermentation. We can use thermodynamics to not only precisely describe what is happening but predict how long each process will take.

A mashing bucket contains a 2 kW heating element in the bottom of it. How long will it take to raise the temperature of four gallons of 15°C (59°F) water to 65°C (150°F) for mashing? We can ask this question and answer it using physics, but first we need to define some words:

• Power of the heating element, p = 2 kW = 2000 W
• Water mass, m
• Specific heat (energy required to raise the temperature of 1 g by 1°C) of water, c = 4.186 J/g K
• Water temperature, T
• Ambient (room) temperature, T_a
• Cooling coefficient (how quickly heat escapes through the bucket's sides), α = 0.20 hr^-1
• Change in time, dt
• Change in water temperature during a change in time, dT

We can now translate some common sense statements into the language of physics. Such as, "The element heats the water by a small amount during a short time interval, but some heat is lost through the sides of the bucket" (Denny, p.96):

 P dt = mc[dT + α(T - T_a)dt]

We can also say, "The change in water temperature over time is equal to the power divided by the energy required to heat up that much water minus the heat lost through the sides depending on the temperature difference":

 dT/dt = P / mc - α(T - T_a)

These two statements merely describe what we can observe. However, the real power and test of a physics model is its ability to predict what will happen. We can use our two statements to ask the question, "What will the temperature of the mash be after t seconds?"

 T(t) = T_a + P/αmc (1 - e)^-αt

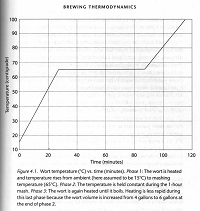
We can also predict how long it will take for the water to reach mashing temperature, T_m = 65°C (150°F):

 Time to mashing temperature, t_m = 1/α ln(P / P-αmc(T_m - Tα) = 27 minutes

As well as predict the time it will then take to heat the mash to boiling:

 Time to boiling temperature, t_b = 1/α ln(P / P-αmc(T_b - Tα) = 29 minutes

We can even predict how much wort we will lose to evaporation during the boil:

 Latent heat of vaporization for water, c_v = 540 cal g/mol
 Evaporation percentage, ε = [P - αmc(T_b - T_a)]/mc_v = 11% or 1/2 gallon per hour (for a six gallon wort)

This now allows us to make a statement regarding the power used during the entire heating process. "The heat supplied by our heating element goes into evaporating the water plus raising the water temperature, as well as heat lost through the bucket wall" (Denny, p.102).

 P dt = εmc_vdt + mc[dT + α(T - T_a)dt]

We boil the wort because it is vulnerable to bacterial contamination below 71°C (160°F) so boiling it kills off any microbes that we do not want turning our wort into spit or snot. Such high temperatures are also quite hostile to the microbes that we do want turning our wort into tasty beer, so we need to cool the wort to 20-37°C (68-99°F) before adding the yeast. Quickly cooling the wort to "pitching temperature" reduces the amount of time bacteria has to potentially take over and can cause suspended proteins will sediment out with a "cold break," but in practice simply covering the wort and utilizing ambient cooling works fine.

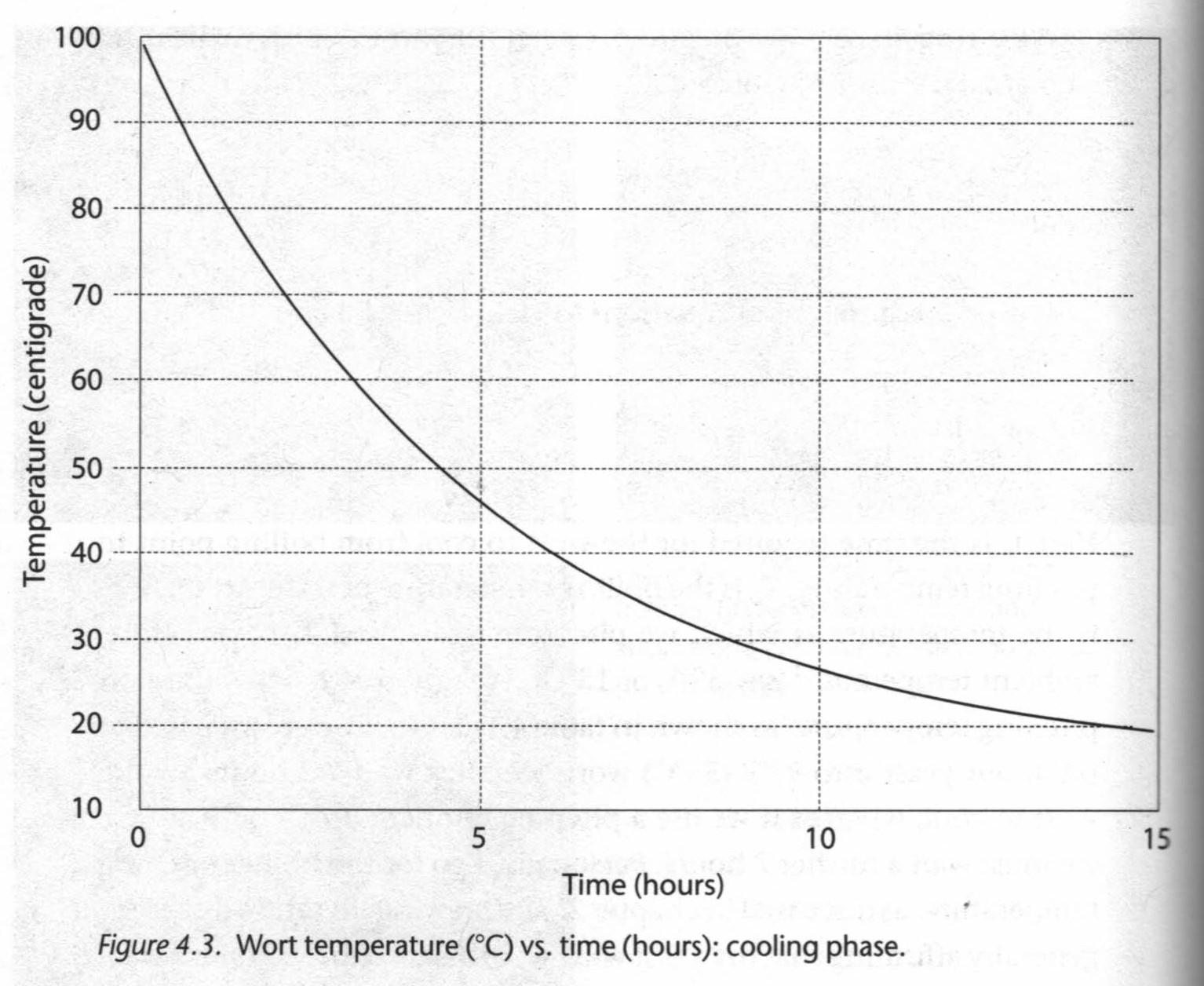
We can describe the cooling process thus:

 Change in temperatue over time, dT/dt = -α(T - T_a)

And then we can predict how long it will take to reach pitching temperature, T_p:

 Cooling time, t_p = 1/α ln[(T_b - T_a)/(T_p - T_a)]

Energy is at the heart of brewing, like it is for most things. Malted barley contains maltose, a sugar consisting of two glucose molecules, and yeast must break the maltose down into glucose before it can start fermentation. It's job during the "lag time" between introduction and fermentation is producing the enzymes that do just that. This requires oxygen, which is why insufficient yeast or oxygen fails to produce good beer: Too much of the maltose remains.

Aerobic yeast respiration looks like this:

 C₆H₁₂O₆ (glucose) + 6O₂ → 6CO₂ + 6H₂O + 688 kcal/mol

Glucose plus oxygen results (after many intervening steps) in carbon dioxide, water, and a lot of energy. Fortunately, most of this energy is used by the yeast for reproduction. If it was waste heat, the temperature of our 6 gallon homebrew would increase by 77°C (139°F), and we'd have steam and dead yeast instead of beer.

Once the yeast consumes all of the oxygen in the wort, they switch to anaerobic respiration. This is what turns the remaining sugar into ethanol alcohol, and it looks like this:

 C₆H₁₂O₆ (glucose) → 2C₂H₅OH (ethanol) + 2CO₂ + 28 kcal/mol

Anaerobic respiration produces much less (only 4%) as much energy as aerobic respiration, which is why yeast reproduces in aerobic respiration but merely survives in anaerobic respiration, so if all of the energy produced by 1 lbs of sugar was waste heat our 6 gallon homebrew's temperature would only increase by 3°C (5°F).

While not all of the energy released by respiration heats the wort, it does result in heating. We can also describe this process using mathematics, but we need to define some more terms first:

• Yeast population p
• Wort volume, V
• Density of yeast cells in the wort, ρ = p/V = constant (for this example)
• Surface area (top and sides through which heat is lost) of the fermentation vessel, S
• Small change in temperature, dT
• Small change in time interval, dt
• Yeasts' ability to generate heat throughout the wort, γ
• Insulating properties of the fermentation vessel, δ = amount of heat lost through the walls
• Cooling coefficient, α = Sδ/mc

Now we can make the statement, "The heat released by yeast catabolizing sugar during a short time interval increases the wort temperature throughout the volume, but some of this generated heat is lost through the surface," (Denny, p. 104):

 Change in temperature, dQ = mc dT = γρV dt = δS(T - T_a)dt

We can also predict the temperature that the wort will reach during the fermentation phase:

 Yeast temperature, T_y = T_a + γρV/Sδ

These statements assume that the yeast population remains constant, which isn't a good assumption. We've seen that yeast population rises exponentially then crashes once it runs out of nutrients. A better statement accounts for changing yeast population. Homebrewers also need to heat their wort during fermentation to keep the temperature within the yeast's comfort range, so we need to add something for this external power supply.

• Time-dependent population, p(t)
• External power supply applied to the bucket after pitching the yeast, P_hb = 30 W for 12 hours

This allows us to make the more complete statement that, "The wort temperature increases due to yeast activity and due to external heating; all the while heat is being lost to the cooler environment," (Denny, p. 106):

 Change in temperature over time, dT/dt = γ/mc p(t) + P_hb/mc - α(T - T_a)