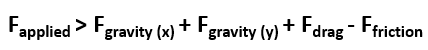Lean In
The true test of Equinox mettle begins at the base of Ester Dome. Five solid miles of straight uphill are followed by a brief respite of three steeply rolling hills over which an additional 600 feet of climbing is required. In reality, the four-mile "out-and-back" is not a respite at all.

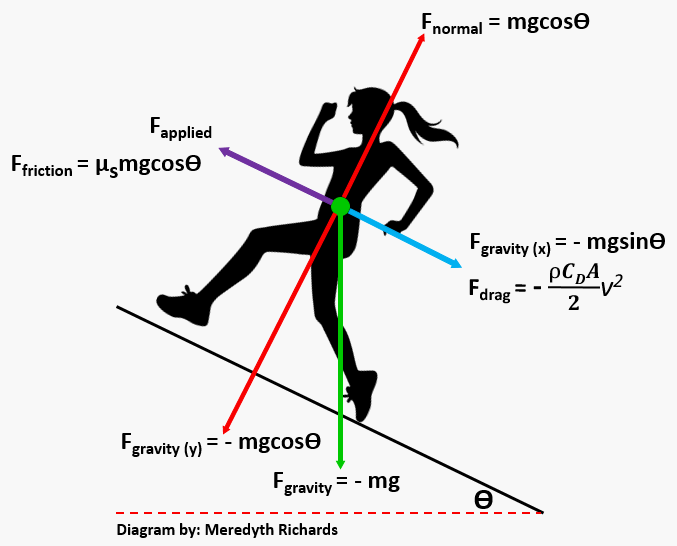
To most efficiently tackle this grueling portion of the course, it helps to consider the force diagram.

 
The forces acting against the runner's progress up the hill are given negative signs whereas those helping her reach the summit are positives. Therefore, to move forward, she must apply a force that meets this criteria:

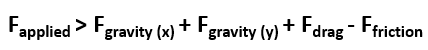
As our own experience with inclined surfaces suggests, more force must be supplied to travel up a hill as the angle of the hill relative to the horizontal increases. In this scenario, not only does the x-component of the gravitational force increase (sin$θ$ approaches 1) but the frictional force helping uphill movement decreases (cos$\theta$ approaches 0). While the y-component of the gravitation force does decrease with a steeper hill, it is not sufficient to overcome the gain in  F_gravity(x) and loss in F_friction. The only force not directly dependent upon the gradient is the drag force. However, as a function of velocity, which tends to decrease while traveling up inclines, F_drag nevertheless indirectly depends upon the hill.

As quantities strictly connected to theta, runners are stuck with the unpleasant forces that result from the geometry of any given hill. Because their desired endpoint is in the opposite direction (up) of the gravitational force pulling them towards the Earth (down), they must do work - in the Equinox, a lot of work - to get up that hill! But by leaning* "into" the hill, shifting the center of mass as far above the front foot as possible, the gravitational force is re-positioned. While the force does not diappear or lessen, when coupled with a planted foot that functions as a fulcrum, the runner's core acts as a forward-rotating load with angular momentum. Although performing this maneuver on an uphill is easier than on a downhill or a flat road (what professional runners attempt), it is still difficult and requires deliberate practice. Even when done perfectly, the extra jolt it theoretically provides is still overwhelmed by the gains and losses of other forces. Yes, it is easier to conquer hills with a forward lean than with a backward lean or neutral body position; no, it is still not easy.

Bear Arms

To help preserve tired legs for  the remainder of the race, arms are an important source of applied force in the Equinox's uphill climbs. Just as they did on rooty and winding trails, swinging arms do still supply the offsetting torque required to maintain directional control. With the more stable footing and straighter uphill route though, arms can more readily move in a purely forward direction and supplement the launching force provided by the runner's legs.

Maximum force from arm movements is achieved when the shoulders are dropped and the elbow is bent around 90 degrees. Because the arm behaves as a pendulum**, the largest velocity for a given mass exists when the length of the pendulum (i.e. distance between shoulder and elbow) is the smallest. When the elbow is held at a constant angle and driven as far back and then forward as possible, the system/arm has the most potential and kinetic energy.  As the kinetic energy increases during the pendulum's downswing, a force is applied by the runner in the direction of motion and positive work is performed, helping them up the hill. The repeated arm pumping required to produce this additional applied force is energy intensive and therefore not an efficient technique for running long distances on flat surfaces. For hills, however, arm pumping economizes the extra energy inherently required during climbs by shifting some of the demand from the legs.

*Biomechanically, it is critical to lean with the hips not bend at the waist. This project is about physics, though.

**Technically, this is a double pendulum. Assuming the angle between the lower and upper arm remains constant, an analogy with a single pendulum seems more accurate.