Faraday's Concepts
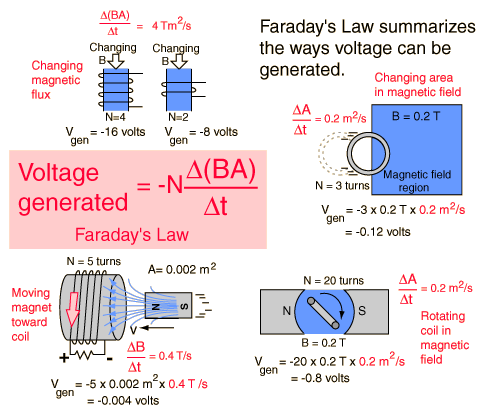
In this image there are four different examples as to how voltage
can be generated.
In the upper left we see that the magnetic flux is equal to the area
inside the wire multiplied by the magnetic field.
Now the voltage generated is directly proportional to the number of
turns around the same area. This is fairly clear with N = number of
turns.
In the upper right hand corner we no longer are changing the number
of turns but instead are changing the area of the magnetic field
with the assumption of three turns. As the area changes in respect
to time the area of the ring within the magnetic field grows at a
rate .2 m^2/s. This isn't any different from a common derivative of
velocity which is dx/dt where dx is the change in position. So, if
this was to stop, there would be no voltage generated.
In the bottom left it demonstrates that voltage can be generated by
a magnet moving toward or away from a coil of wire. The area and
number of turns are constant however, B, the magnetic field changes
as it gets closer to the coil. If you were to move the magnet away,
this would create a negative voltage.
The lower left demonstrates a magnet that is turning a .2 m^2/s
within a field that is .2 T and there is 20 turns of coil. Here, the
rotation changes the perpendicular area of the coil with respect to
the magnetic field
