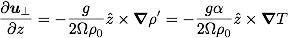Flows due to a thermal gradient
Thermal wind in a rotating tank
The temperature gradient sets up flows due to convective cells. These flows are influenced by the Coriolis effect due to the rotation. A simple setup involves placing a can filled with snow and ice from outside in the center of the rotating tank. The rotation rate is about 1 rpm. Dye is added for flow visualization.
Observations from the experiment in the rotating tank shows that the velocity at the bottom rotates in an opposite sense as the flow on the surface. This can be interpreted as the temperature gradient driven flows being influenced by the Coriolis effect.
As seen in the above video, the fluid moves in two directions. The bottom surface moves in a clockwise fashion while the top layer moves in the anti-clockwise direction. In the bottom layer, colder fluid moves from the center of the tank to the periphery of the tank. However, the warmer fluid moves from the periphery to the center. As a result, a velocity shear is induced in the vertical direction.
The variations in the horizontal velocities are due to the temperature gradient. Expressed in cylindrical coordinates, the relation is
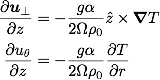
This means that the variation in the azimuthal velocity comes from the radial temperature gradient. Hence, in order to demonstrate the variation in the azimuthal velocity, the rotation rate needs to be small. In this experiment, the tank rotates at 1 rpm. With a large rotation rate, the multiplying fraction in front of the temperature gradient decreases, which reduces the induced sheared azimuthal flow.
Thermal wind equation
Small density variations due to a temperature gradient affects the geostropic flows. This allows the fluid move vertically, which alters the two-dimensional constraint of geostrophic flows. The horizontal density variation is modeled to be small,
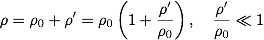
Then, this density is substituted back into the equation for geostrophic flows. The z-direction derivative is taken, and the hydrostatic vertical balance is used. The resulting equation for vertical variation in the horizontal velocity components are
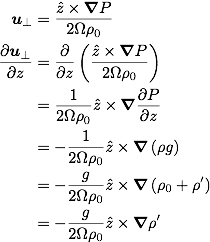
By assuming a linear dependence between the small density variation and temperature,

the vertical variation in the horizontal flows relate to the density variation by