Flows due to a thermal gradient
Geostrophic flows in a rotating tank
Fluid in a uniformly rotating frame of reference exhibits peculiar behaviors. One of them is the balance between a horizontal pressure gradient and the Coriolis effect. The horizontal sense is taken to the plane perpendicular to the rotation. Flows generated within this regime are called geostrophic flows.
In order to demonstrat this regime in the tank, the rotation rate is about 20 rpm. The water in the tank must achieve a solid body rotation before performing the experiment. This takes about 10 min for the current tank size. Dye is added for visualization. And, the rotation rate is decreased slightly by about 1 rpm to induce a small horizontal flow.
Obstacles are placed on the bottom of the tank to show the constraint on the fluid motion along pressure contours (forming Taylor columns). The constrained motion in a two-dimensional plane results from the balance of the pressure gradient and the Coriolis force. In effect, the fluid moves two-dimensionally without a change in the vertical velocity component.
As part of a class discussion, an open question whether geostrophic flows can exist over a dip or indentation is also explored in this experiment. A circular hole is drilled into a separate plexiglass and elevated over the bottom.
In reference to the video above, a dark colored dye is added to the rotating tank over a circular dip and a circular obstacle. Taylor columns can be seen to exist over the circular dip with the red colored dye. Mixing happens when the dye in the bottom boundary layer enters the dip. On the other hand, the Taylor columns over the obstacle do not portray the Taylor-Proudman theorem.
Geostrophic flow equation
Starting with the momentum equation for an incompressible, inviscid, baroclinic fluid,
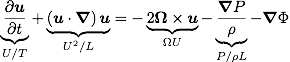
The Rossby number is defined as
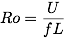
where the Coriolis parameter is defined in terms of the angular rotation and the Earth's latitude as
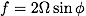
In terms of the rotating apparatus, the latitude is 90 degrees, which reduces to the usual form for the Coriolis effect. The Coriolis effect dominates when the Rossby number is much less than unity. So, the momentum equation is reduced to geostrophic flows using the ordering argument from the Rossby number,

The significance of these flows is that the flow is two-dimensional along pressure gradients. The flows shown are for velocity components perpendicular to the rotation (z-direction).
In terms of horizontal components, the geostrophic flows are
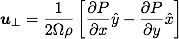
With the incompressibility constraint, the vertical velocity can be shown to vanish,
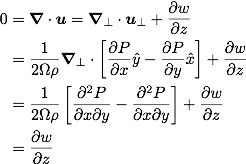
This results leads to the Taylor-Proudman theorem. Under slow, steady, and frictionless barotropic flow, the flow velocities perpendicular direction do not vary in the rotational direction. In this flow regime, fluid parcels form Taylor columns.
In the rotating direction, the equation yields the hydrostatic pressure balance,
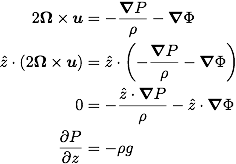
One of the requirements for geostrophic flows is that the Rossby number must be less than unity. In order to achieve this criterion, the rotation rate must be large enough while the induced flow velocity must be small.