Ekman Layer Derivation and Mathematical Formulation
Ekman Number:
The Ekman number is the ratio of the eddy viscosity the rotation rate and scale depth squared:This dimensionless quantity can be obtained in the same way the Rossby number is obtained: we divide the momentum equations with viscosity and rotation (x direction shown):
![]() ,
,
by the angular flow velocity:
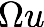 .
.
The last term in the momentum equation,
when divided by the angular flow velocity, yields the
Ekman number (consider scale heights as H). We
use this dimensionless quantity to define a scale height
for the Ekman layer. Inside the layer, the Ekman number
is larger than 1; outside the layer, it's less than one.
The Ekman layer scale is set at the depth to give an
Ekman number 1 (note that a factor of the square root of
two may be present, depending on the derivation):
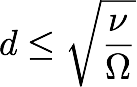 .
.
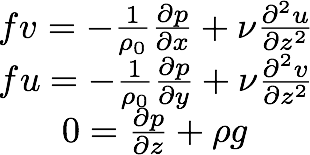 ,
,
For ocean water we have viscosity
~10^-2 m^2 s^-1 and rotation rate ~10^-4 s^-1,
yielding an Ekman layer ~10 m. Please note that in a
system like the earth, the rotation rate used should
be the Coriolis parameter f.
Ekman Layer Dynamics:
Now that the height of the layer is known, we describe what happens in this layer. Lets take, for example, the interface between two layers of fluid, the only difference between layers being the steady state flow velocity. Above a height d, there is a constant and uniform flow velocity u (we can assume it's in the x direction, or transform our coordinate system until it is) and below the height d there is no flow (again without loss of generality, Galilean transform our coordinates system into the frame of the fluid in the bottom). Since the flows are steady and uniform in the vertical direction, any time or vertical space derivative is zero. The momentum equations are a slight modification of the standard geostrophic version: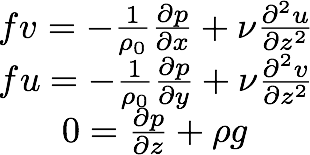 ,
,and the continuity equation is
simply the incompressibility assumption:
 .
.
The boundary conditions give
us the character of the solutions:
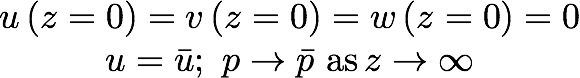 .
.
In the upper region,
where the fluid is flowing uniformly, we
have:
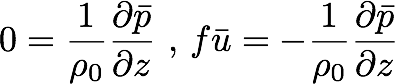 ,
,
and these in the momentum equations give us:
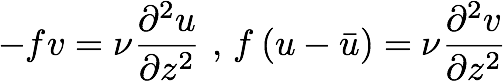 .
.
Solutions to these are of the form:
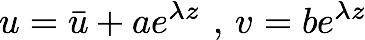 ,
,
and these in the momentum equations give us:
Solutions to these are of the form:
with a and b
constants and eigenvalue allowed to be
complex. Plugging in this form to obtain
the eigenvalues gives:
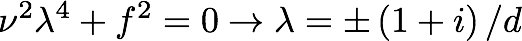 .
.
Some of the solution is physical and some is not, since we know the velocity cannot diverge as the vertical height increases. In fact, we know that the y velocity goes to zero and the x velocity goes to the average velocity in the top part of the fluid as height z increases. Considering this and taking values of a and b that provide physical solutions yields:
 ,
,
with d the previously discussed Ekman boundary scale. The resulting flow is turned 45 degrees to the left of the average x flow velocity in the upper fluid. Keep in mind this derivation was done for Coriolis parameter larger than one; in the southern hemisphere, the resulting flow would be turned 45 degrees to the right. This turning of the velocity as vertical height increases tends to create a spiral of flow, lovingly called the Ekman spiral.
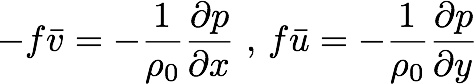 ,
,
we obtain the solutions for the Ekman flow in this layer:

Integrating over the entire vertical expanse of our fluid yields the transport:
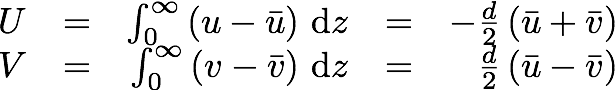 .
.
In the beginning of this derivation, we began with a geostrophic flow assumption that the horizontal divergence of the horizontal flow is zero. Is this transport due to the Ekman flow divergence-free too?
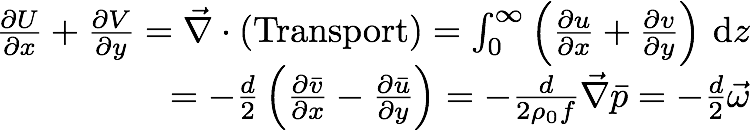 .
.
The divergence of the Ekman transport depends on the vorticity of of the bulk (average) flow of the fluid above. If the fluid above has a nonzero vorticity, there is divergence in the horizontal transport. Please note we also made the assumption that the fluid was incompressible. In order to have a horizontal divergence and maintain incompressibility, there must be a vertical flow! This vertical flow is called Ekman pumping and has velocity:
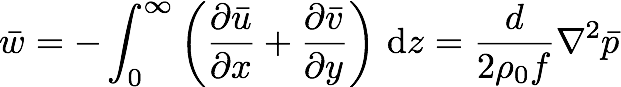 .
.
Neat!
Some of the solution is physical and some is not, since we know the velocity cannot diverge as the vertical height increases. In fact, we know that the y velocity goes to zero and the x velocity goes to the average velocity in the top part of the fluid as height z increases. Considering this and taking values of a and b that provide physical solutions yields:
 ,
,with d the previously discussed Ekman boundary scale. The resulting flow is turned 45 degrees to the left of the average x flow velocity in the upper fluid. Keep in mind this derivation was done for Coriolis parameter larger than one; in the southern hemisphere, the resulting flow would be turned 45 degrees to the right. This turning of the velocity as vertical height increases tends to create a spiral of flow, lovingly called the Ekman spiral.
Ekman Transport:
The above derivation was for uniform flow in the upper fluid, but in general this is not the case. If we do the same derivation for a nonuniform flow, with average velocities in the upper fluid being:we obtain the solutions for the Ekman flow in this layer:
Integrating over the entire vertical expanse of our fluid yields the transport:
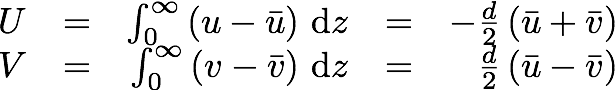 .
.In the beginning of this derivation, we began with a geostrophic flow assumption that the horizontal divergence of the horizontal flow is zero. Is this transport due to the Ekman flow divergence-free too?
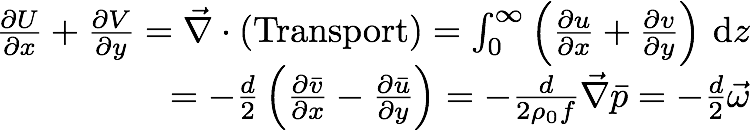 .
.The divergence of the Ekman transport depends on the vorticity of of the bulk (average) flow of the fluid above. If the fluid above has a nonzero vorticity, there is divergence in the horizontal transport. Please note we also made the assumption that the fluid was incompressible. In order to have a horizontal divergence and maintain incompressibility, there must be a vertical flow! This vertical flow is called Ekman pumping and has velocity:
Neat!
Table of Contents:
- Abstract
- Derivation and Mathematical Formulation (this page)
- Historical Observations
- Visualization and Experimental Observations
- Resources