After escaping earths atmosphere things get a little bit easier on the rockets performance and the physics side, first there is no air resistance or turbulence to try to fight meaning there is no forces to have to counteract to maintain a constant velocity or acceleration. If close to earth the force of gravity is still a very real thing needing to be accounted for, to go into an orbit around earth the rocket would need to essentially free fall in a way that it would continuously "miss" earth and orbit it. For this to happen we need gravity to pull the rocket towards the center of the earth while traveling fast enough tangentially to not actually hit earth. If we have a force of gravity pulling radially inward at toward earths center we can model that with g = ma_r, where a_r is the radial acceleration equal to the velocity squared over the radius of the orbit.
g = mv²/r
Based on Newtons laws of motion we know that g = GM/r² so we can now solve this equation to find the tangential velocity needed to achieve circular orbit around earth. v = sqrt(GM/r)
Now this is just a simple case of orbital mechanics that is used when launching rockets to find the optimal acceleration needed to get to the optimal velocity for desired orbit, but these can also be applied to other planets when their gravity wells are reached. This can also be applied partially for acceleration boosts from massive bodies with large gravitational pulls, if a satellite is getting close to mars it could position itself such that as it flies by its velocity is high enough to not get pulled into orbit around mars but slow enough to where its trajectory is affected by the gravitational pull adding some acceleration as it goes by and is sort of sling-shotted by it giving it more acceleration.

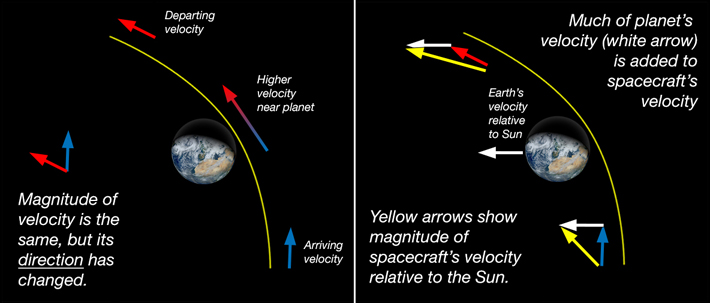
This picture shows how a gravity assist would work on earth.
Greicius, Tony. “Juno Earth Flyby.” NASA, NASA, 26 Aug. 2013, [8]

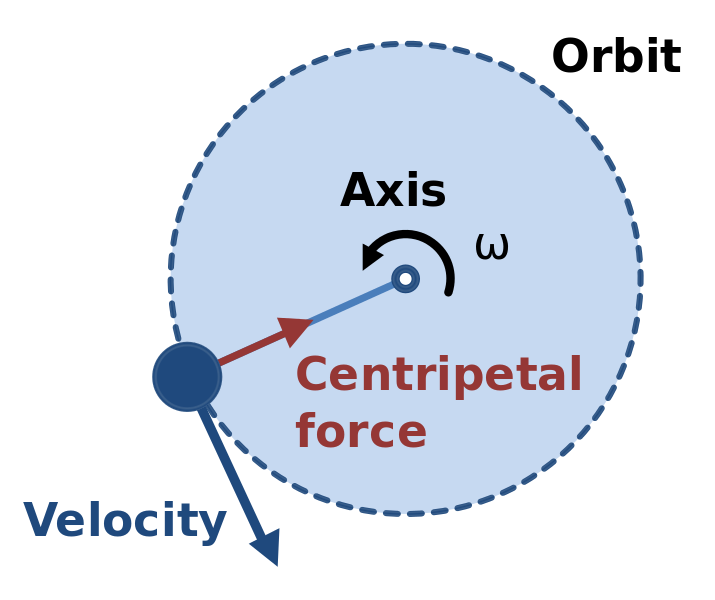
This picture gives a visual representaion of the above equation for orbit.
Wiki User: Booyabazooka. Centripital Force. Nov. 2008.