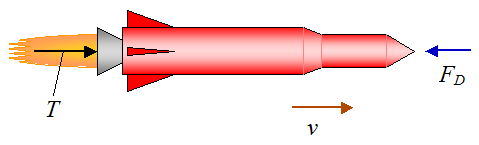
Inside of a rocket the physics gets much more complex and interesting as it begins to convert the chemical energy of the fuel into mechanical energy producing thrust. Now if we look at the energy for a rocket moving through the air, we can use Thermodynamic equilibrium equations
and Newtons equations of motion to derive the math behind it. First we define the work(Wr) needed to push our rocket a distance(d) with a thrust force(T).
Eq(1). (Wr = T * d)
Since the engine is just a more complex design of a heat engine, we can apply the energy equation using heat and work.
If we have a rocket moving at velocity(v), an exhaust mass(me), an exhaust velocity(vp), and the work(we) required to convert the energy of the propellant over a distance(d) we can work out the equation.
Eq(2). 0.5*mev2+We = 0.5*me(v-vp)2
We can then define our thrust(T), using a constant burn rate(R) in terms of the change in mass(dme) per change in unit time(dt), multiplied by our exhaust velocity(vp)
Eq(3). T = (dme/dt)vp = Rvp
If we know the mass of the rocket and there is a constant burn rate(R) of fuel then (me = R * t), if we put this into our energy balance equation as well as our equation for the work of the rocket(Wr)
Eq(4). Etot = Wr + We = R(vp)2d/(2v)a
Which can also be written as Etot = Tvpd/2v
Since this is the energy for a constant velocity rocket that would mean the thrust force and the drag from air resistance will be equal for no acceleration. First the equation for drag(FD), using the drag coefficient(C) the density of air(p), the cross sectional area(A) of the rocket perpendicular to our velocity direction, and the velocity(v) of the rocket.
FD=1/2CpAv2
Plugging this into our energy equation we get the total energy needed to move the rocket over a distance.
E = 1/4CpAvvpd