Leavitt's Period-Luminosity Relation http://www.angelfire.com/gail.bischoff/auit/variable.html $m_v-M_a=5log_{10} (d) - 5$ Calibration allowed the absolute magnitudes of Cehieids to be logarithmically quantified in large groups with the "Distance Modulus" formula; $m_v - M_a = 5log_{10} (d) - 5$ With data from a pair of Cepheids having the same period of variance, "the one with the Greater average magnitude is the star that is nearest to us" (Star). 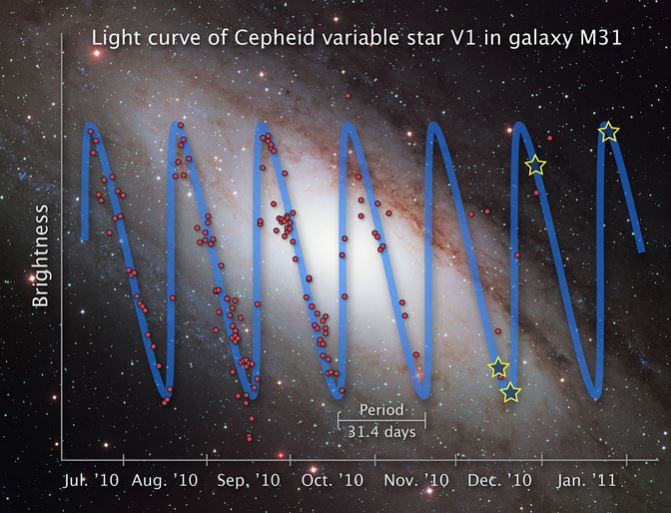For Example: red dots - Observations by the American Association of Variable Star Observers, (AAVSO), from July to December 2010 (NASA, 2011). The Hubble Telescope uses a mirror that is 2.4 meters across to capture images. We can determine how bright a star in from its period thanks to Leavitt! Period = 31.4 days If the luminosity log-log plot corresponds to aprox. 16,000 times the sun. Sun's luminosity =  $3.85*10^{26}$Watts. $V_1=(16000)(3.85*10^{26}=6.16*10^{30} [W]$ We can now find the distance to the star using flux (F) = $1*10^{-15} [W/m^2]$ (Flux: how much light is hitting each square meter of our telescope) and the Flux-Luminosity (L) relationship: $F=\frac{L}{4\pir^2}$ Solving for distance we have: $r=[\frac{L}{4\pi F}{]}^{0.5}=[\frac{6.16*{10}^{30}}{4\pi *{10}^{-15}}{]}^{0.5}=2.21*{10}^{22}\mathrm{m\; <br>}$ In light years that is $2.42 * 10^{22}$ light years which is close to the accepted distance reported in $Hor=[\frac{L}{4\piF} ]^{0.5}= [\frac{6.16*10^{30}}{4\pi*10^{-15}}]^{0.5}=2.21 *10^{22}m$

Index -- Leavitt 1 -- Leavitt 2 -- Leavitt 3 -- Leavitt 4 -- Leavitt 5 -- References