These equations will allow you to effectively determine the efficiency of the turbine and generator at hand.
Turbine
efficiency is given by: Ƞ= (mechanical energy output)/(mechanical
energy decrease of the fluid)
Generator
efficiency is given by: Ƞ= (electric power
output)/(mechanical power output)
The
combined efficiency is of a turbine and generator is
given by:
Ƞturbine-gen=ȠturbineȠgenerator=(electric
power output)/(mechanical energy decrease of the fluid)
Total
Energy Equation
Like I
said before we can treat turbines as steady flow devices
because they operate under the same conditions for long
periods of time. No intensive or extensive
properties change withint the control volume, so the
volume (V) and total energy
content (E) will remain constant. As a result of this
the boundary work is zero
for steady flow processes. These observations greatly
simplify the analysis.
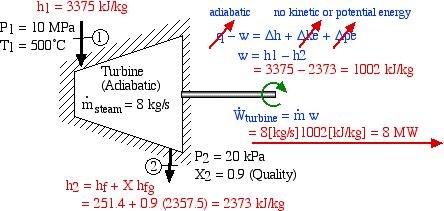
This image above represents a common turbine
problem
The fluid properties remain constant at the inlet and exits, so this means the mass flow rates (ṁ) must remain constant too.
ṁ1= ṁ2 ρ1V1A1 = ρ2V2A2 The dot above the letter represents rate
Total
energy content
Ein=Eout
This equation is used mostly to find your power output of the turbine
Q̇in+ Ẇin + ṁ(h+V2/2+gz)= Q̇out+ Ẇout + ṁ(h+V2/2+gz) V is for velocity, z is for height,and h is for enthalpy
For turbines this equation simplifies nicely
Heat transfer is negligible so Q̇=0 since turbines are well insulated and can be labeled adiabatic
The fluid velocities encountered in turbines are very high, and the fluid experiences a significant change in kinetic energy. However, this change is usually very small relative to the change in enthalpy, so its disregarded.
The total energy for turbines then reduces to this
ṁ(h+V2/2+gz)= Ẇout + ṁ(h+V2/2+gz)
Solving for Ẇout we can determine power output