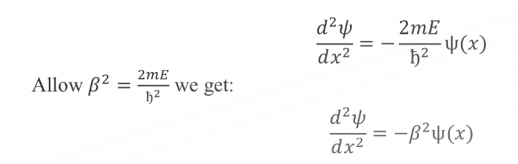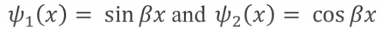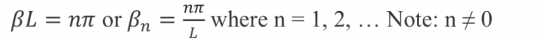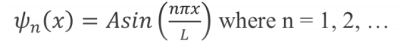Let’s start by restating that U(x) = 0 within the region of the box, thus the Schrödinger’s equation becomes.

Solving using second order differential equations we produce two family functions,

where both are solutions to our original second order differential equation. As a result our general solution is

Where A and B are constants and when our initial conditions are applied such that x = 0 the function also must equal zero, only the Sin function remains because cos(0) = 1, and even though it is mathematically possible we know from our established boundaries this cannot be.

Now we must solve for when x = L which also has to give us zero for a function value.

If sinβL=0, then

So the Schrödinger equation of family solution becomes