Practice #2 Location and probability
A particle with the quantum number n = 1 is in a rigid box of let’s say length L, where can we most likely find this particle and what is the likeliness of locating this particle with width of L being 0.01L at x = 0.00L, 0.25L, and 0.50L, also how likely are you to find the particle between .25L and .75L? (text)
First when the quantum number is n = 1 the probability density models:
(ground state probability density)
Note the probability density is maximum at the max crescent which is x = L/2
Secondly the likeliness of finding the particle with an interval of length pretty small becomes
First when the quantum number is n = 1 the probability density models:
(ground state probability density)
Note the probability density is maximum at the max crescent which is x = L/2
Secondly the likeliness of finding the particle with an interval of length pretty small becomes
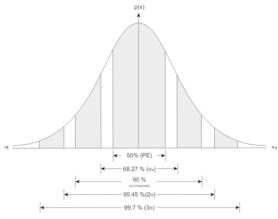
Reasoning: as we observed in the probability density diagram and experiences from calculus a likeliness of 81.8% is realistic for a wave function of this kind. We can also observe that the probability of locating the appearance of this particle in the ground state is when x =L/2 which is the place where the crescent is maximum, and the locations where the particle is least likely to appear is at x = 0 and x = L. Notice how both of these insights are concepts introduced in the wave particle duality, which we have shown to be true (in most cases).

