Relativity’s New Horizons
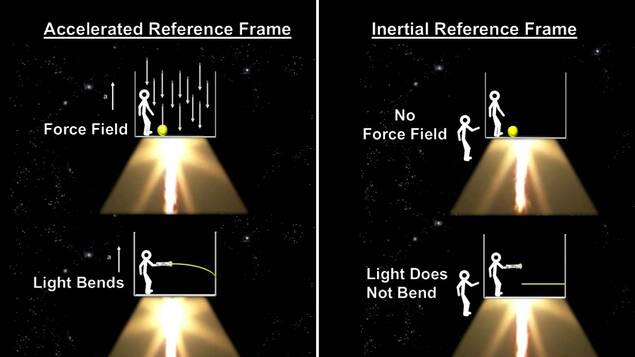
Einstein's Equivalence Principle
Since special relativity only dealt with inertial frames of reference, many physicists believed that there was a more general form of special relativity. So, the hunt for general relativity began. In 1907, Einstein began with a concept known as the equivalence principle, believing that there is no physical distinction between accelerating in free space and the force inflicted by gravity. For example, if an observer is in an accelerating box in space, free of gravitational fields, there is no experiment that the observer can do to prove that they are accelerating in free space or to prove if they are in the presence of a gravitational field.
Einstein's Field Equations
Einstein proposed that space-time, where time is a pseudo-dimension of space is curved, meaning it can be represented by matrices and geometric equations. But since tensors, a mathematical expression of matrix algebra, represent spatial dimensions, the dimension-like time was introduced. This also was due to time seemingly being dependent on space, and so was considered another term of space, hence space-time. After many years, in 1915, Einstein devised the Einstein Field Equations relating the curvature of space-time with the mass, energy, and momentum within the space around it. Space-time can be expressed as a mathematical equation.
Where R𝜇𝜈 is the Ricci curvature tensor, R is the scalar curvature, g𝜇𝜈 is the metric tensor, Λ is the cosmological constant, G is Newton's gravitational constant, c is the speed of light in vacuum, T𝜇𝜈 is the stress–energy tensor.
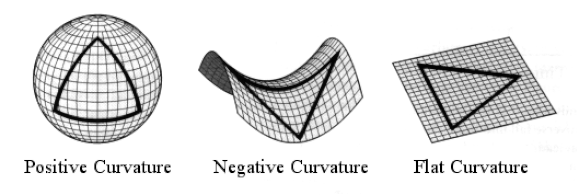
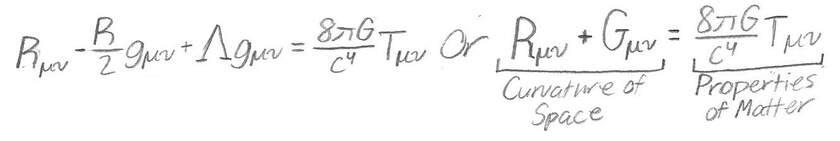
With these equations and the equivalence principle, the math leads to even weirder consequences than special relativity. Similar to time dilation, gravitational time dilation means that time runs slower the deeper an observer goes into a gravitational well. A gravitational well being a region in space that becomes significantly curved by a massive object such as stars, black holes, and even planets. When masses rotate, especially massive objects, the space-time around them is dragged along with the mass. The metric tensors, the variables with subscripts, are a description of the topology of space-time, the study of bending and warping, and how objects move around these space-time curves.