The Physics Of Aerobatic Flying

Contents

• Home
• Dynamics Of Flight
  • Turns
  • Forces Of Flight
  • Derivatives Of Position
  • Left Turning Tendencies
    • Torque
    • P-Factor
    • Spiraling Slipstream
    • Gyroscopic Precession
• Aerobatic Maneuvers
  • Rolls
  • Loop
  • Hammerhead
  • Torque Roll
• Bibliography

The Loop

The loop is a simple maneuver to learn, but complex to preform perfectly. It simply involves starting from level flight and pulling the airplane up through a complete circle in the sky. Though this may sound easy (and on a very basic level, it is), the complicating factors are that a loop that is to score highly in a competition must:

•Enter and exit at the same altitude

•The airplane must not change heading (direction) during the loop

•The airplane must not lose speed during the loop (within reason)

•The loop must be circular, not egg or cursive 'l' shaped.

These requirements certainly add difficulty to the loop, but any aerobatic pilot worth their salt can preform a loop to all of these requirements. What this means is that we can calculate various attributes of loops using equations from Chapter 8 (Motion In A Plane) without having to excessively "assume away" factors like friction or a slightly elliptical path.

Some Initial Information For Calculations

Typically, if I am going to practice a loop as a single maneuver (i.e. not chained together with others in a sequence), I use a setup like the following:

•Initial entry airspeed: 145 miles per hour

•Acceleration at the bottom of the loop: 3.5 g

•Acceleration at the top of the loop: 0 g

•Airspeed at the top of the loop: ~40 miles per hour

What is interesting to note here is that the airplane is simply acting as a projectile at the top of the loop because it is free falling, or experiencing 0 g. Though a coincidence, this makes this problem exactly like those in the textbook. Practically, this is because pulling more g at such a low speed would stall the wings.

What is the diameter of the loop?

Since the airplane is experiencing 0 g at the top of the loop, this means that the normal force at the top of the loop is 0 N. This would allows us to use the very simple equation that relates the critical speed of this loop to the radius and g:

                           

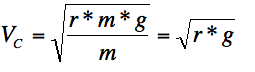
    Before we insert values, we need to convert units for Vc:

    •Vc = 17.88 m/s

Now, solving the equation for r, we find that r=32.62 meters, or 107.02 feet. Multiplying by two, this means that the loop will have a diameter of about 214 feet.

However, comparing the altitude of a loop at the bottom and top in a video:

We can see that the diameter is actually about 500 feet. What caused this difference? Ignoring forces such as drag, the main issue with this simple calculation is that it fails to account for the fact that the object looping is a lift-producing airplane at the bottom of the loop, not a simple particle. Additionally, it fails to account for the large force of the propeller "pulling" the airplane up the sides and over the top of the loop. Factoring in these forces would, unfortunately, make the problem much more complicated, so we will have to accept this "spherical cow" calculation.

Physics 211