The Physics of Paintball

Time for Distance

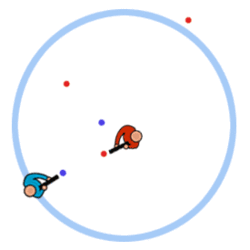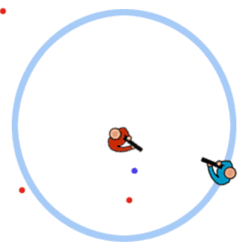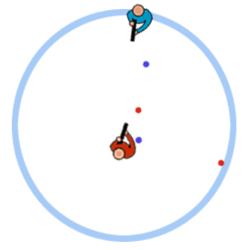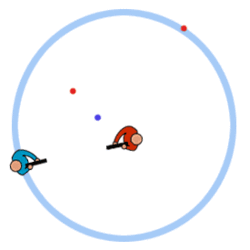
This page shows how long it will take for a paintball to mark it's target at varying distances. This is important for two main reasons. It tells you how early to fire your marker in order to hit a target (likely moving) and it tells you how long you have to move out of the way of a paintball that was fired at you. In the animation below, the red player is doing a bad job at predicting where the blue player will be by the time the paintball reaches it's target and the blue player is doing a good job at moving out of the way of the red player's paintballs.

In order to determine the time it will take for the projectile to reach it's target, the following equations must be solved for t.

$x = \frac{v_{o}v_{t}\cos\left (\theta \right )}{g}\left (1-e^{\frac{-g t}{v_{t}}} \right )$
$y = \frac{v_{t}}{g}\left (v_{0}\sin\left (\theta \right ) + v_{t} \right )\left (1-e^{\frac{-g t}{v_{t}}} \right ) - v_{t}t$

Where x will be replaced with the distance to the projectile's target and y will be set to zero (assuming the target is at the same height as the paintball marker). It is likely that there will be several solutions, this is because there are different angles at which the projectile can be launched to reach the target distance. The projectile can be fired at a lower angle to take a shorter arc path, reach the target faster, and have more impact, or it can be fired at a higher angle to take a longer arc path, reach the targer slower, and have less impact.

This should help:

Distance (meters)	Time (seconds)
0	0.00
10	0.11
20	0.22
30	0.33
40	0.45
50	0.57
60	0.68
70	0.81
80	0.93
90	1.04
100	1.18

Notation:
$v_{t}$ : the terminal velocity of the projectile
$m$ : the mass of the projectile
$g$ : the gravitational acceleration on the projectile
$\rho$ : the density of the fluid through which the object is moving
$A$ : the projected area of the object
$C_{d}$ : the drag coefficient of the projectile
$a_{x}$ : the projectile acceleration in the x direction
$a_{y}$ : the projectile acceleration in the y direction
$t$ : the time difference from when the projectile is launched
$v_{x}$ : the projectile velocity in the x direction
$v_{y}$ : the projectile velocity in the y direction
$v_{o}$ : the initial velocity at which the projectile is launched
$\theta$ : the angle at which the projectile is launched
$v$ : the magnitude of the sum of the x and y velocity vectors
$x$ : the distance from the origin in the x direction
$y$ : the distance from the origin in the y direction
$F_{ave}$ : the average force on the projectile
$\Delta v$ : the change in velocity of the projectile
$\Delta t$ : the difference in time
$\Delta d$ the difference in position of the projectile
$Impulse$ : the change in momentum of the projectile

Contsants:
$m=3.201*10^{-3}kg$     (average mass of a paintball)
$g=9.81\frac{m}{s^{2}}$     (gravity on earth)
$\rho = 1.164\frac{kg}{m^{3}}$     (air density at 1 atm and 30 degrees celcius)
$A = 2.343*10^{-4}m^{2}$    (cross sectional area of a paintball)
$C_{d} = 0.47$     (drag coefficient for a smooth sphere)
$\empty = 0.017272m$ (diameter of a paintball)