|
|
|
Lift :
To
understand the exact mechanism of lift in case of a flying animal, it
is easier to first treat the aerodynamics in a relatively simpler
manner. Studying the movement of an object through a fluid is
equivalent to studying the flow of the fluid about a stationary object,
in terms of fluid dynamics. This is the Lagrangian
viewpoint, as opposed to the Eulerian
viewpoint.
Let
a cylinder with circular cross section (of radius b) be immersed in a
fluid flowing with a constant velocity u. Now, if the
cylinder starts to rotate (with spin s rad/sec), it can be shown that
the cylinder experiences a lift! And, the lift per unit length of the
cylinder is given by L = r
G u.
Here,
G ( = 2 p b Vr
) is the circulation,
Vr ( = 2
p b s) is
the rotational speed of the cylinder,
r
is
the fluid density.
A rotating cylinder
immersed in a steady fluid flow (Ref: http://www.nasa.gov/centers/glenn/home/index.html )
The coefficient of lift is defined as
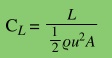
with A being the area of the surface over which the fluid flows, and r being the fluid density.
The
Mathematics
(our tool
to comprehend nature's intricacies) :
From the condition
of continuity in a fluid, flowing with velocity u, ∇. u
= 0.
With this condition satisfied, the flow can be described by a
streamfunction, Ψ, such that the streamlines are lines along
which Ψ is constant. The radial velocity(ur) and
angular velocity (uΘ) are then given by (in polar
co-ordinates)
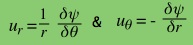
If the flow is irrotational, or the vorticity is zero, then ∇ X u = 0.
Another function, Φ, better known as the velocity potential, can be
derived from this equation, such that,

A complex function, w(z), can be defined as w = Φ + i ψ. w(z) is
called the complex potential.
Now, if a constant flow, with a clockwise (hence, negative)
circulation, -Γ, is considered around a stationary cylinder, the
resulting complex potential looks like
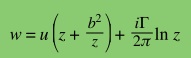
Hence, taking the imaginary part of w to get ψ, and then differentiating it
yields uΘ.
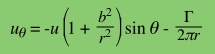
The value for uΘ
at
r = b can be determined from this equation. It may also be noted
that ur= 0 at r=b.
The fact that this expression for the angular velocity at the surface
of the cylinder gives rise to a pressure, is obtained from Bernoulli’s
equation, which states that,
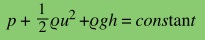
where p is the pressure, r
is the
density, and h is the given height for the fluid.
Hence, considering that ur= 0 at r=b, and that there is no
horizontal pressure due to symmetry, the vertical component of the
pressure can be integrated to get the lift per unit length of the
cylinder :
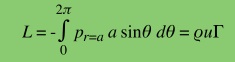
Now, it needs
to be noted that, the above expression for lift is valid not just for
cylinders with circular cross sections, but for all other cross
sections as
well!
The
following applet illustrates this point. You may change the input option to "Shape/Angle", and
then vary the option just underneath the movie to "airfoil",
"cylinder", etc. To enjoy more of the fun, play with all the other
options!
No
wonder, then, that animals with wings, the cross-sections of which
resemble air foils, can sail through air!
Web Project by Debasmita Samaddar
PHYS 645, University of Alaska
Fairbanks
Fall - 2007
source for template
-> Free web templates
|
|



