Drag :



                There are actually a number of drags that come into play during flight. However, when we refer to ‘drag’, we generally mean a sum of all the drag forces.

The coefficient of drag is defined as




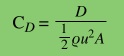
with A being the area of the wing surface, D is the drag, and r being the fluid density.

The different drag forces are :


Viscous Drag :    The boundary layer on the surface of the wing has zero velocity, while there is freely flowing fluid at the other end (the top) of this layer. This results in a shear, and the drag results from the fluid’s resistance to this shear.



Pressure Drag or Inertial Drag : As an object moves through a fluid, it generates a turbulent wake behind it. The pressure in this wake is lower than that in the front, thus resulting in a backward pull.



With l taken as the width of the wing, and  m being the dynamic viscosity, such that, n=m/r is the kinematic viscosity, the Reynold's number defined as


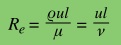
For R_e < 1     viscous drag is important
       R_e > 1     pressure drag is important



The lift increases with the angle of attack (the angle (a) between the chord and the direction of flight) till the stall angle is reached. Beyond the stall angle, the wake behind the wing becomes turbulent, causing an increase in drag - and this is called stall.

So, the angle of attack cannot be increased indefinitely to enhance lift!

The stall angle is typically 20° for birds, 30° for grass hoppers and 50° for fruitflies.






Induced Drag :  This drag is the ‘price’ for the lift. The lift is perpendicular to the direction of motion of the wing. Hence, when the wing is not horizontal (that is, there is a non-zero angle of attack), the horizontal component of the lift acts as a drag, while the upward component works against the gravitational pull.


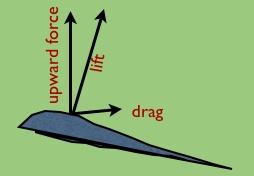
As the tip vortices contribute in tilting the wings further, they cause an increase in the induced drag.

However, in practical situations, the induced drag is much smaller than the vertical component of the lift.


The aspect ratio may be defined as L = s/c
where  s is the wing span (distance between wing tips) and c is the average chord length.

Higher the aspect ratio, lesser the tip vortices. Thus, long, slender wings will have lesser induced drag. But, this, too, has a limitation. Flying amidst tall trees, with very long wings, is also not the most acceptable idea!