Stability
- I
Equilibrium
and
stability:
In dynamics,
‘equilibrium’ means – no change in
motion. So, if a moving body is in equilibrium, it cannot have any
acceleration.
Either it is at rest or it moves at uniform velocity.
To understand ‘stability’
we can consider a ball at rest ( in equilibrium, obviously). We want to
know, how
stable its equilibrium is. Let us consider the ball in three different
situations as shown in the diagram.
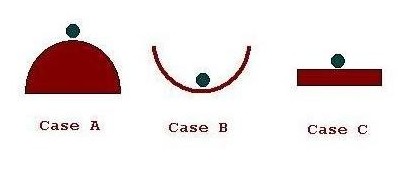In case-A,
the ball is kept on the top of an
inverted bowl. In case-B, the
ball is inside the bowl and in case-C,
the ball
is placed on a plane surface.
Three different
things are observed in these
situations:
- If we now
displace the ball slightly, in the case A, the ball displaces ifself
further. So, it is said to
be in unstable equilibrium.
- In case-B, the
ball, when displaced (slightly),
goes back to its previous position and so, this is the case of stable
equilibrium.
- In case-C, the
ball, when displaced, neither can
goes back to the previous position, nor does it go away from that
location. So, we
call it to be in neutral
equilibrium .
Stability in
(static) atmosphere:
We may observe an
air parcel in the atmosphere. At a
certain position z = z0,it
is part of the atmosphere and its density is ρ0 . So, it’s
weight
(the force due to gravity) per unit volume is ρ0g. This
air-parcel is now displaced to z = z1,
where the density of the surrounding is ρ1.
At this point, we should renew our knowledge about
buoyancy. Buoyancy is the
force that
is applied by a fluid, on a body that is immersed in it. This buoynat
force develops
due to the fluid-pressure on the body.
The fluid-pressure on the top(downward) of the body is always less than
that on
the lower-face (upward). The reason is simple, - the top side is always
at a
smaller depth than the bottom. Due to this difference in pressure, the
buoyant
force acts in the upward direction, trying to counterbalance the force
of
gravity.
The force of
buoyancy, on a body in a fluid, is
equal to the weight of the fluid that is displaced by the body itself.
So, if the
parcel we are observing doesn’t mix with its surrounding, then the net
force F
on it, per unit volume, is:
F = (ρo – ρ1)g.
We define
stability S as,
S = (ρo- ρ1)/(zo – z1) when,(z – z1)-> 0
or, S
= -(dρ / dz)
Comparing with the previous examples
for explaining
stability, we can say that the parcel is :
- Stable if S > 0, or
positive.
-
Unstable if S
<
0, or negative.
- Neutral
if s = 0
A
better atmospheric-model:
Stability in a
polytropic atmosphere:
This model is
more realistic because it fits the atmospheric properties better.
Assumptions: the
process is adiabatic, which ensures that
the parcel under consideration does not exchange heat with its
surroundings.
It can be derived
that for a polytropic atmosphere :
ρo / ρ1 = (po – p1)1/n
where, n is some
index. Now, the stability factor S
can be shown to be depending on the
relative value of n as compared to γ, the ratio of two specific heat of
the
fluid (here, air). So,
- If
n
< γ Stable
as S > 0, or
position.
- If
n
> γ Unstable
as S<0, or
negative.
- If n
= γ Neutral as
S = 0.
Tapas
bhattacharya
Web-project
: Phys-645, Fall-2007, UAF
Animation
for 'Home" - taken fromwww.animationlibrary.com
