The Physics Behind the Cantenna

The Cantenna - A Physics 632 Web Project

Go to the table of contents

The physics of a Cantenna is quite complicated and in practice most people use a simple applet to calculate the dimensions of the can needed. This will be covered in the How to Build section of this website. Here I will work a graduate level physics problem that is similar to our Cantenna problem. If you are not at least a graduate level physics student, there is a good video explaining the general idea on the Links page. If you can follow this, it is a simple matter to move to the Cantenna problem, which is an exercise I will leave to the reader ( you don't learn anything it I just do it for you).

This problem is problem 8.19 in John David Jackson's Classical Electrodynamics, Third edition, which is a really good resource for all things electromagnetic. Chapter 8 covers Waveguides, Resonant Cavities, and Optical Fibers. On with the Problem:

8.19

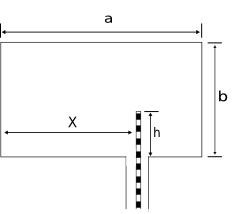
The figure below shows a cross-sectional view of an infinitely long rectangular waveguide with the center conductor of a coaxial line extending vertically a distance h into its interior at $ z = 0$. The current along the probe oscillates sinusoidally in time with frequency $ \omega$, and its variation in space can be approximated as $ I(y) = I_o\sin[(\omega/c)(h-y)]$. The thickness of the probe can be neglected. The frequency is such that only the $ TE_{10}$ mode can propagate in the guide.

Image f8-19

(a)

Calculate the amplitudes for excitation of both TE and TM modes for all $ (m,n)$ and show how the amplitudes depend on $ m$ and $ n$ for $ m,n \gg 1$ for a fixed frequency $ \omega$.

Solution to part (a)

(b)

For the propagating mode show that the power radiated in the positive z direction is

$\displaystyle P = \frac{\mu c^2 I^2}{\omega k a b} \sin^2 \left( \frac{\pi X}{a} \right) \sin^4 \left( \frac{\omega h}{2c} \right) $

with an equal amount in the opposite direction. Here $ k$ is the wave number for the $ TE_{10}$ mode.

Solution to part (b)

(c)

Discuss the modifications that occur if the guide, instead of running off to infinity in both direction is terminated with a perfectly conducting surface at $ z = L$. what values of L will maximize the power flow for a fixed current $ I_0$? What is the radiation resistance of the probe (defined as the ration of power flow to one-half the square of the current at the base of the probe) at maximum?

Solution to part (c)