Jackson Problem 8.19 (a)
The Cantenna - A Physics 632 Web Project
Calculate the amplitudes for excitation of both TE and TM modes for all  and show how the amplitudes depend on
and show how the amplitudes depend on 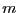 and
and 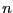 for
for 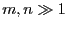 for a fixed frequency
for a fixed frequency 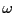 .
.
except when where
where
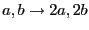 as the constant mode averages to
as the constant mode averages to 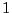 , not
, not 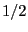 .
.
and as
where we have made sure to use the normalization appropriate for an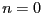 mode in
mode in
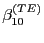 .
.
For TE modes, we know that
| (1) | ||
| (2) | ||
| (3) | ||
|
where
| ||
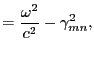 and and  |
||
|
and when normalized
| ||
 |
||
except when
For TM modes, we know that
| (4) | |||
 |
(5) | ||
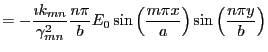 |
(6) | ||
|
and when normalized
| |||
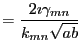 |
|||
and as
The excitation amplitudes are
 |
(7) | |
|
where
| ||
| (8) | ||
|
Hence
| ||
![$\displaystyle = -\frac{Z_{mn}}{2}I_0\int^h_0 \sin \left[ \frac{\omega}{c}(h-y))\right] E^{(\mp)}_{y,mn}(X,y,0)dy$](./Pictures/img37.png) |
(9) | |
|
Taking the integral gives
| ||
![$\displaystyle = \beta_{mn}^{(TM,TE)} \sin \left( \frac{m\pi X}{a}\right) \left[...
...s\left[ \frac{n \pi h}{b} \right]- \cos \left[ \frac{\omega h}{c}\right]\right)$](./Pictures/img38.png) |
(10) | |
|
where
| ||
| (11) | ||
|
since at large m,n the wave number is imaginary as all TM modes are cutoff modes. Likewise
| ||
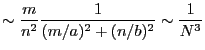 (TE) (TE) |
(12) | |
|
as all the modes are cutoff for
| ||
![$\displaystyle = \beta^{(TE)}_{10} \sin \left( \frac{\pi X}{a}\right) \left[1- \cos \left( \frac{\omega h}{c}\right) \right]$](./Pictures/img43.png) |
||
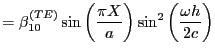 |
(13) | |
where we have made sure to use the normalization appropriate for an