Jackson Problem 8.19 (c)
The Cantenna - A Physics 632 Web Project
Discuss the modifications that occur if the guide, instead of running off to infinity in both direction is terminated with a perfectly conducting surface at 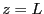 . what values of L will maximize the power flow for a fixed current
. what values of L will maximize the power flow for a fixed current 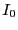 ? What is the radiation resistance of the probe (defined as the ration of power flow to one-half the square of the current at the base of the probe) at maximum?
? What is the radiation resistance of the probe (defined as the ration of power flow to one-half the square of the current at the base of the probe) at maximum?
where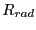 is the radiation resistance.
is the radiation resistance.
Placing a perfectly conducting surface at ![]() will cause the right moving wave to be perfectly reflected at this surface. Then the wave flowing out the left side will be a linear superposition of the left moving wave generated by the probe and the reflected wave. Since the parallel component to the electric field at the surface of a perfect conductor must vanish, the reflected wave will come back
will cause the right moving wave to be perfectly reflected at this surface. Then the wave flowing out the left side will be a linear superposition of the left moving wave generated by the probe and the reflected wave. Since the parallel component to the electric field at the surface of a perfect conductor must vanish, the reflected wave will come back ![]() out of phase. We can write the left moving wave as
out of phase. We can write the left moving wave as
| (16) | ||
|
and it is easily seen that the reflected wave must be
| ||
| (17) | ||
|
so that at
| ||
| (18) | ||
|
The maximum amplitude case occurs when there is constructive interference
| ||
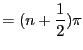 |
(19) | |
|
since the amplitude doubles, the power is then increased by a factor of four. For this maximum power case, the radiation resistance is given by
| ||
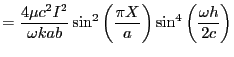 |
(20) | |
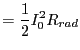 |
(21) | |
where