Jackson Problem 8.19 (b)

The Cantenna - A Physics 632 Web Project

Go to the table of contents
For the propagating mode show that the power radiated in the positive z direction is

$\displaystyle P = \frac{\mu c^2 I^2}{\omega k a b} \sin^2 \left( \frac{\pi X}{a} \right) \sin^4 \left( \frac{\omega h}{2c} \right) $

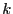with an equal amount in the opposite direction. Here $ k$ is the wave number for the 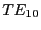$ TE_{10}$ mode.

The radiated power is

$\displaystyle P^{(\pm)}$ $\displaystyle = \frac{1}{2 Z_{mn}} \left\vert A^{(\pm)}_{mn} \right\vert^2$ (14)

Using the amplitude from (13) for the $ TE_{10}$ mode, we find


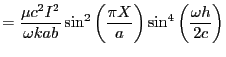$\displaystyle P^{(\pm)}$ $\displaystyle = \frac{\mu c^2 I^2}{\omega k a b} \sin^2 \left( \frac{\pi X}{a} \right) \sin^4 \left( \frac{\omega h}{2c} \right)$ (15)

We can see here that the Power transmitted depends upon the dimension's of the wave guide. In order to find the right dimension's you would find the maximum of this equation.

Solution to part (c)