 |
|
|
Home
Page
A
little history about Kirchoff
A
little history about Ohm
Kirchoff's
current and voltage laws
Ohm's
law
Circuit
analysis example
Bibliography
It's time for the nitty-gritty. Let's define Kirchoff's Current and Voltage Laws:
First Kirchoff's Current Law.
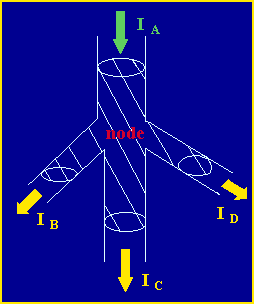
Kirchoff's Current law can be stated in words as the sum of all currents flowing into a node is zero. Or conversely, the sum of all currents leaving a node must be zero. As the image below demonstrates, the sum of currents Ib, Ic, and Id, must equal the total current in Ia. Current flows through wires much like water flows through pipes. If you have a definite amount of water entering a closed pipe system, the amount of water that enters the system must equal the amount of water that exists the system. The number of branching pipes does not change the net volume of water (or current in our case) in the system.
http://www.physics.uoguelph.ca/tutorials/ohm/Q.ohm.KCL.html
Now, Kirchoff's voltage law.
Kirchoff's voltage law can be stated in words as the sum of all voltage drops and rises in a closed loop equals zero. As the image below demonstrates, loop 1 and loop 2 are both closed loops within the circuit. The sum of all voltage drops and rises around loop 1 equals zero, and the sum of all voltage drops and rises in loop 2 must also equal zero. A closed loop can be defined as any path in which the originating point in the loop is also the ending point for the loop. No matter how the loop is defined or drawn, the sum of the voltages in the loop must be zero.
