Exploring
Solar Sails
Solar Sails | The math behind solar sails
Introduction | Solar Sail Physics
Solar sails harness light photons on a large surface called a sail. When light hits the reflective layer of a solar sail there is a force applied to the solar sail due to the lights enormous speed. Lasers can also be used to propel a solar sailed powered spacecraft. When the photon hits the reflective layer, most of the photons bounce off the perpendicular to the sail surface. The photons that are not reflected are absorbed, then emitted though the emissivity layer in the form of thermal energy which has a negative effect on the spacecraft's speed as it produces a negative effect. It is important to note that solar sails are extremely dependent on light as a source of fuel, the further you get away from the light source the less efficient the sails become because less photons hit the sail. If there is very little light intensity, the sails will accelerate at a slower rate than before. When there are no photons hitting the sail, the spacecraft will still travel through space, but without acceleration, it will decrease in speed, becoming extremely slow because space is not 100% vacuum. For instance, Jupiter has about 1/24 the amount of light intensity of Earth, so a spacecraft by Jupiter would have to be 24x larger to produce a similar force of a solar sail close to Earth. Solar sails have a maximum speed which is 10% the speed of light, which equates to 18,600 miles per second or, 67,100,000 mph. Solar powered spacecrafts are able to travel faster than conventional rocket fueled spacecrafts due to constant light pressure being applied to the sail propelling it forward.
Diagrams | Light reflecting off Solar Sail
Reflection Layer
Case 1:
Reaction Force
Reaction Force
Light Source
Initial Momentum
Reaction Momentum
Solar Sail
Emissivity Layer
Case 2:
Light Source
Solar Sail
Initial Momentum
Reaction Momentum
Reaction Force
Reaction Force
Reflection Layer
Emissivity Layer
Forces and Momentum | How it works
Initial Momentum
The initial momentum is the momentum of protons from a light source. This momentum applies a force into the solar sail.
Reaction Momentum
Reaction momentum is the reaction from the initial momentum from the light source. The reaction momentum is always perpendicular to the solar sail's surface, as seen in case 2 diagram.
Reaction Force
The reaction force is thermal energy which is due to the solar sail being heated up. The emissivity layer emits thermal heat, which creates a reaction force which is a negative force on the spacecraft trajectory.
Solar Sail
The solar sail is the spacecraft's propulsion that holds the reflection and emissivity layers.
Reflection Layer
The reflection layer is the material that faces the sun or incoming light, this surface reflects incoming photons and also takes in heat due to a reflective value less than 1.0 which is a perfect reflection.
Emissivity Layer
Emissivity layer faces away from the light source powering the solar sail. This layer emits thermal energy.
Physics | Calculations
Force of a Solar Sail | Calculating
Calculations to find the force of a solar sail.
Perfect Sail:
Nothing is perfect in our universe, a more realistic sail would have an equation similar to:
Realistic Sail:
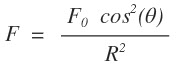

Momentum | Light Particles
Reflectivity Scale
Perfect Absorbent
Perfect Reflection
0.0
0.25
0.50
0.75
1.0
Common reflection values of solar sails 0.88 to 0.90
Light has an extremely small mass, basically zero, but it has an incredible high velocity. With such high, velocity light partials or photons have momentum.
Momentum of 0.0 reflectivity surface
Solar sails have a reflective layer which reflects the light particle, which produces even more momentum as it pushes off the reflective layer.
Momentum of 1.0 reflectivity surface


Force | Solar Sail
As momentum hits the solar sail it gives off a force, this force value is based on the reflectivity value of the reflective material and solar energy that hits the solar sail
The problem here does not take into account for gravitational forces, non perfect reflective surface, emissivity layer, and estimated atmospheric drag.


Velocity | Calculating the Velocity
Initial equation used to find velocity

Moving dv to the right side of the equation


Statement that dp = mdv
Substituting mdv into the equation and mulitple the momentum by a factor of 2. This is due to the reaction momentum
Solving for dv
Substituting
dV = LA
L = ct c = speed of light
t = time in seconds
substituting the speed of light into the equation and canceling one c in numerator

Let's assume the following for a spacecraft who just left earth, m = 70 lbs, using one large solar sail with a surface area of 124x124 feet and the sails are perfectly reflective.

Now we will plug in the numbers.

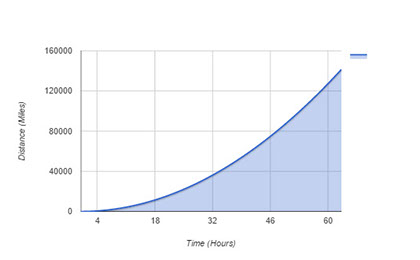
From this we can make a table for how long it will take to reach certain velocities.
Velocity
Time
Distance Traveled
1 m/s
3.793 min
0.1414 miles
50 m/s
3.16 hours
353.52 miles
100 m/s
6.32 hours
1,414.12 miles
500 m/s
31.61 hours
35,352.9 miles
1000 m/s
63.21 hours
141,411.62 miles
Distance vs Time