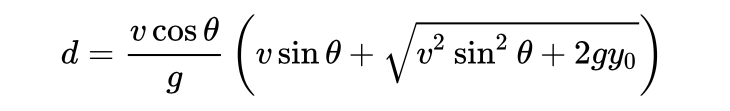The pressure builds, the hot fumes spiral around the bullet as its ejected from the barrel of the gun, angular momentum attempts to hold the bullets course despite all external forces working against it.

Barrels graphic ​maritime.org

Barrel rifling from thefirearmblog.com

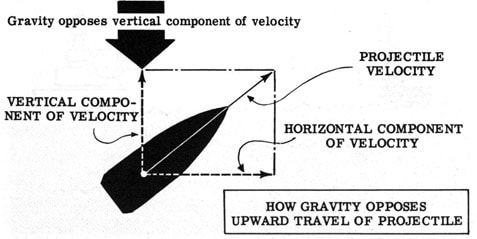
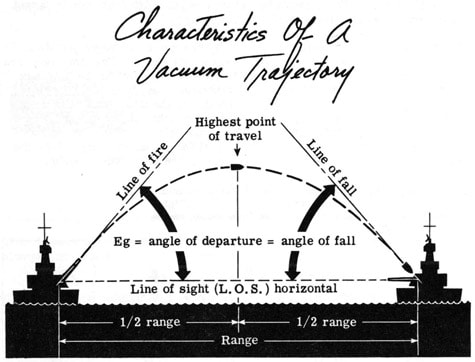
Where a bullet lands is determined by more factors than just momentum. As the target moves farther away from the marksmen, acceleration due to gravity increases bullet drop, wind and air currents create friction on the bullet and the random spin of the projectile creates bullet drift, all of which pull the projectile off of its course. To compensate, guns both large and small, artillery and handheld, must use some form of barrel rifling and elevation to compensate for unwanted external forces.

Angular Momentum

Rifling in many barrels allows air to spiral through the curved grooves which in turn spins the bullet to provide more accuracy as the bullets trajectory is stabilized. The speeding body of the bullet due to rifling imparts angular momentum on the bullet, which is responsible for a major increase in the accuracy of a bullet over a longer distance. Angular momentum refers to the amount of rotation in the bullet and is characterized by its resistance to rotation. 

---

This rotation can be quantified by using the equation L=I*W, which means the angular momentum vector acting on the bullet is the product of its moment of inertia and the angular velocity of the bullet. We can decompress this formula by substituting I and W for their respective values on the right, and subsequently come up with the formula L=r*m*v. Angular momentum equals radius times mass times velocity.

---

Gravity

Though wind resistance and gravity both affect the travel of a bullet, gravity will remain constant in most conditions besides a massive change in elevation.

​To calculate where a bullet would fall in a vacuum, you would first have to break velocity up into its X and Y components to find the angle at which the projectile was fired.

As the shooters distance from the target increases, so does the bullets angle of departure, which means at what angle above the target does the shooter have to aim to still hit the target.

In cases of great range or many guns, the initial velocity of the projectile would also become a factor. In reality the initial velocity of a bullet can't be changed besides packing a bullet with more powder such as +P ammo, but in particular for a warship that has many sized guns, not all guns may be able to fire at a target given the range.

Explaining the forces affecting a bullet in a vacuum.

The application of the distance formula for the range of a projectile.

/ L = I * W
/ I = R^2 * M
/ W = (V / R)
/ L = R * M * V

---

---

Bullet leaving barrel.  imgur.com

South Cushman Shooting Range, Fairbanks.

Air Friction

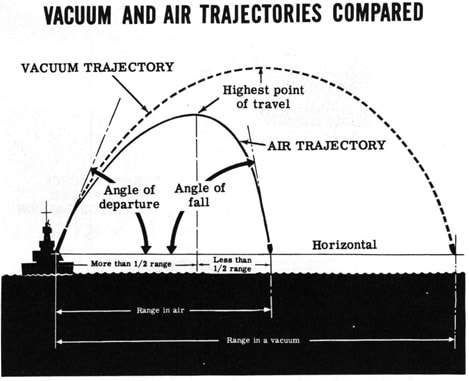
The friction of air or wind on a bullet has wide ranging implications for bullet drift, but for simplicity's sake I will only be covering the downward forces of air friction and not the inclusion of potential cross wind scenarios. In the graphic to the right, air has a great impact on how far a bullet travels.

---

The initial velocity of the projectile is affected by very little wind resistance due to its high velocity, but overtime wind resistance will have an increased affect on the object. With this understanding we can conclude that the longer a projectile remains in the air, the greater its trajectory will be altered by wind resistance.

How wind interacts with a bullet.

Demonstrating how air or a lack of air affects how far a bullet travels.