Plucking vs Bowing
There are 2 main ways that you can
produce sound on a string instrument, you can either pluck the
string or use a bow.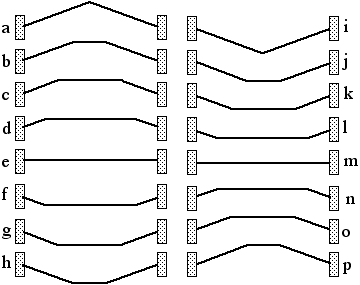
Fig. 1. sketch of what happens when a string
is plucked, from Joe Wolfe Strings, Standing
Waves and Harmonics; 2016.
Plucked
As shown in fig.1, when a string is plucked
it has "pulse wave that propagate[s]" in both directions from
where it was plucked (Rossing, 2014). The resulting vibration
is what we hear, and it can be considered as a "combination of
several modes of vibration" (Rossing, 2014). What is meant
by that is, if the string is plucked from the center, the
vibration is a mix of "the fundamental plus the odd-numbered
harmonics" (Rossing, 2014); and if the string is plucked from
any where other than the center it will have a mix of the
modes it is made of, and thus will sound different to us.
Since there are so many options, we can find the speed
(corresponding to the sound we hear) of the resulting sound
wave using this equation:Vsound,string = sqrt(T/µ)
where T is the tesion and µ is the mass per unit length (sqrt mean square root) (McGill, 2017).
Bowed
When one uses a bow,
instead of just plucking, a few things about our waves
change. Fisrt off, the string now has "continuos energy"
so now it can continue it's motion indefinitely (lets
pretend we will never run out of bow) (Wolfe, 2016). Also,
the shape of the string that is required to match the
uniformely moving bow is different as well.
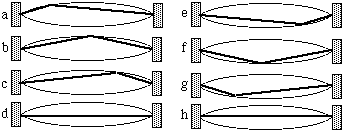
Fig. 2. A sketch of the reflection of travelling kinks
caused by bowing a
string, from Joe Wolfe, Strings, Standing Waves
and Harmonics; 2016.
Another intersting thing is that a string actually doesn't
just vibrate back and forth. In actuality, the string
"forms two
straight lines with a sharp bend at the point of
intersection", as seen in fig. 2, and the bend moves
around that curved path we see (Rossing, 2014).