Harmonics

On string instruments, since they are mostly fixed on both sides, any vibration must have nodes on each side, which limits the possible vibrations. This brings the about the modes of vibration, which we can then look at the frequencies of. When we look at the relationship between the frequencies we find that
    "The fundamental or first mode has frequency of f₁=v/2L
     The second harmonic has a frequency f₂= 2f₁
   The third harmonic has a frequency f₃= 3f₁    The fourth harmonic has a frequency f₄=4f₁, and, to generalize
The n^th harmonic has a frequency f_n=nf₁" (Wolfe, 2016)

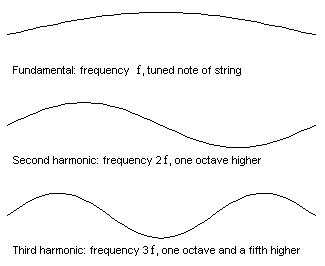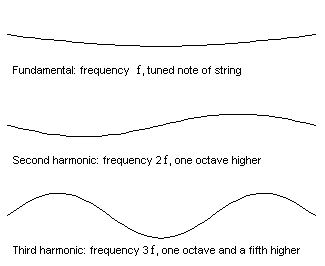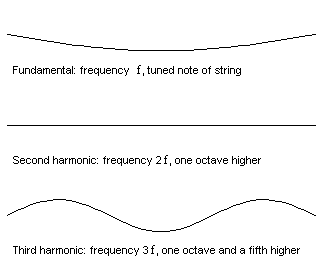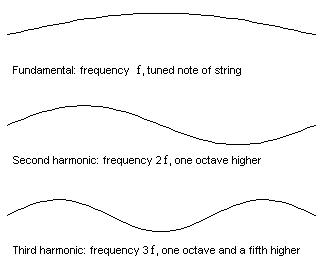
Fig. 1. Different harmonic frequencies, from N/A; What Are the First,
Second Etc Modes of Vibration?, 2016

All of the modes are also called harmonics of the string and the frequencies f, 2f, 3f, 4f, etc. are called the harmonic series. You can produce these pitches on a stretched string (violin, viola, cello, etc.) by touching your finger lightly at a point 1/n of its length from the end, then bow the string close to the end, this also works with plucking.

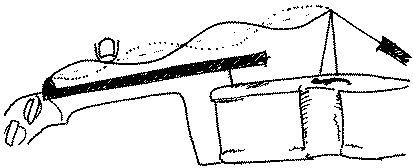
Fig. 2. Depiction of what a "touch fourth" harmonic is, from Joe Wolfe; Strings, Standing Waves and Harmonics. 2016

Often times composers will call for the use of harmonics in pieces of music as well. The most commonly used harmonic is called the "touch fourth"; where a player will stop the string will put down one finger at the length required for a particular note, then they will use another finger to touch the string very lightly in a position that is 4 notes higher in the scale. For those who play string instruments harmonics are called "natural" when they are played on an open string and "artificial" if they must stop the string.

                                     Fig. 3. a "touch fourth" as it show up in
                                     music, from Joe Wolfe; String, Standing
                                    Waves and Harmonics. 2016