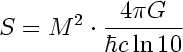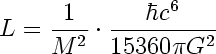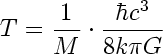Brentley Powell - Black Hole Physics

Homepage  Fundamentals  Relativity  Thermodynamics  Resources


  Thermodynamics


        In 1970, Stephen Hawking made a breakthrough contribution to black hole physics. He observed that Quantum Mechanics describes the region around a black hole as emitting particles at a constant rate. Hawking was able to prove that that quantum fluctuations near the surfaces of black holes could radiate to an arbitrarily large distance. For this to happen, the black hole would have to absorb negative energy, decreasing its mass. This was the discovery of hawking radiation, the process of black holes emitting black-body radiation.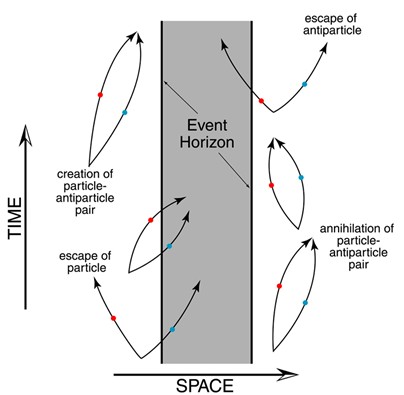

Quantum fluctuations near event horizons release hawking radiation.
(from http://minerva.union.edu/diiorios/physics123/moreinfohawkingrad.html)


        Physical systems are subject to the laws of thermodynamics. According to the Second Law of Thermodynamics, the entropy within a closed thermodynamic system increases over time. Entropy is a measure of the amount of hidden information within a system. It quantifies the uniformity of distribution or disorganization within a system. Entropy has units of Joules/Kelvin (Energy per unit temperature), but it can also be a dimensionless number used to represent quanta of information. The second law implies that over time, more and more energy is required to do an amount of work.

        Black holes have extremely high entropy. Technically speaking, entropy relates to the number of possible micro states described by the macro state of a system. Since black holes are fundamentally simple objects, they hide an enormous number of possible configurations within their horizons. Throwing matter into a black hole is an extremely efficient way to increase net entropy as almost all information about the matter is hidden from the outside. In fact, the thermodynamic entropy of a black hole is known to be directly proportional to its surface area, which increases proportionally to the square of mass.
Entropy, S, of a black hole
(from http://xaonon.dyndns.org/hawking/)

        Modern physics provides formulae which relate fundamental constants and units to the thermodynamic properties of black holes. (see below)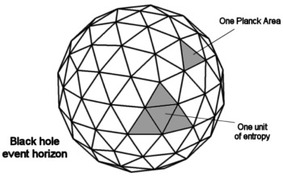

 
Four plank areas on an event horizon account for one unit of entropy.
(from http://www.scholarpedia.org/article/Bekenstein-Hawking_entropy)

(The following formulae were sourced from http://xaonon.dyndns.org/hawking/)

M - mass, kg
h-bar - plank's constant / 2pi
G - Newton's gravitational constant
k - Boltzmann's constant
c - speed of light
Lifetime, t, in seconds
Luminosity, L, Watts
Temperature, T, Kelvin

        The lifetime of a common black hole is finite, yet incomprehensibly long. Even a small black hole of 10 solar masses would take more than 2.0x10^70 years to evaporate, whereas the current age of the universe is merely 1.37x10^10 years. The same black hole would have a power output of 9.0x10^-31 Watts, and a temperature of 6.167x10^-9 Kelvin. Cold objects produce little black-body radiation. Considering that background radiation is significantly greater than this, black holes are not shrinking any time soon.



See Resources for full list of sources.