Surviving a Suicide Burn

In-case you've never heard of a suicide burn before, here's a video of someone cutting it close to smashing into the moon in KSP:                               https://youtu.be/iKZKXhN00sM?t=1m35s

Time is money, and when you are a college student creating a website for your physics 211 class you don't want to waste any time getting down to the surface of that lumpy rock. Using the kinematic equations for motion we can calculate the minimum height above the surface to start our engines.

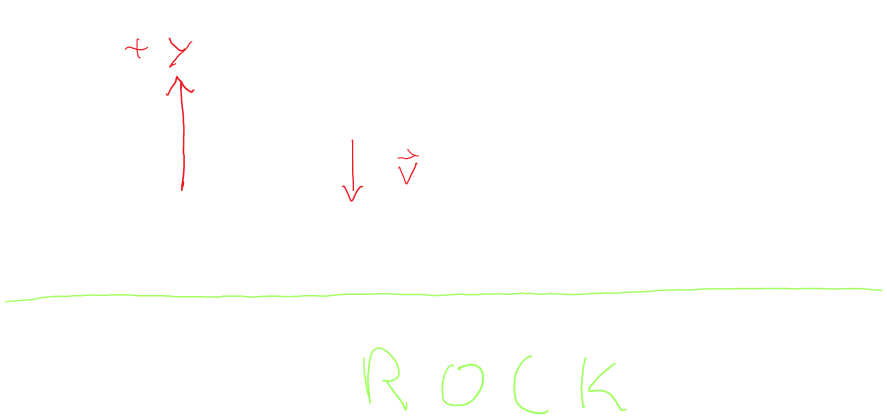
Firstly, To better Understand our problem we can draw some diagrams. The first diagram shows our lander in its predicament rushing toward earth. The second zoomed view shows the forces acting on our lander; force thrust, and force gravity.

Because we have some initial velocity to deal with we will have to use some time burning to bring that to zero. Additionally, we will need to consider how the force of gravity is accelerating and account for that as well.

These are the Kinematic Equations. notice how the 4th equation relates initial velocity with final velocity and change in X. In our case, delta X will be the minimum height to start our engines from and our final velocity will (hopefully) be zero.  Because Force = mass * acceleration (Newton's Second Law of Motion) we can sum the forces acting on our lander and divide by its mass to calculate the acceleration. Now that we have all the variables defined we can solve for minimum height.

How Close Is Too Close?

Let's say you've got a capital ship and need to get to the other side of a planet A.S.A.P., you can't go though it so in order to shave off some travel time how close can we get without the pull of gravity taking over...