The Physics of Ski Travel on Glaciers
A great example of glacier
travel that is both convenient and necessary is the Kahiltna
glacier in the Denali state park. Climbers, Mountaineers, and
skiers utilize the longest glacier in the Alaska Range to
access peaks like Denali, Hunter, and Foraker. The low angle
slopes with no trees, a glacier like this is ideal for landing
bush planes and building base camps.
These same features also make glaciers prime for ski touring. Ski touring is when you have a special binding that allows your ski boot to have a free heel and pivot on the toe. A type of "skin" is then put on the base with an adhesive. The skins have small hairs on the bottom that allow the ski to be easily pushed in the forward direction, but not the backwards direction. Skis like this are most popularly used to access ski areas that lack a lift, but they are also necessary for any ski mountaineering. They are very similar to a snowshoe, but the forward glide and dual purpose make them much more practical. You can think of the Kahlitna Glacier as the highway and the skis as your vehicle for access the peaks in the Denali area.

Image Courtesy of backcountry.com
The first step is to figure out the coefficient of friction of your ski skin. The easiest way to do that is to find a slope with a known angle and bring a pack and various weights at a constant acceleration. You then go up the hill with increasing weight until the skins no longer provide sufficient friction (You slip). The calculation would be fairly straight forward. Lets assume Joe wanted to try this in his back yard where there is a 30 degree hill. He finds that his skins no longer can hold his weight on the slope when he has a total mass of 80 kg with his pack when he accelerates at 2 m/s^2.
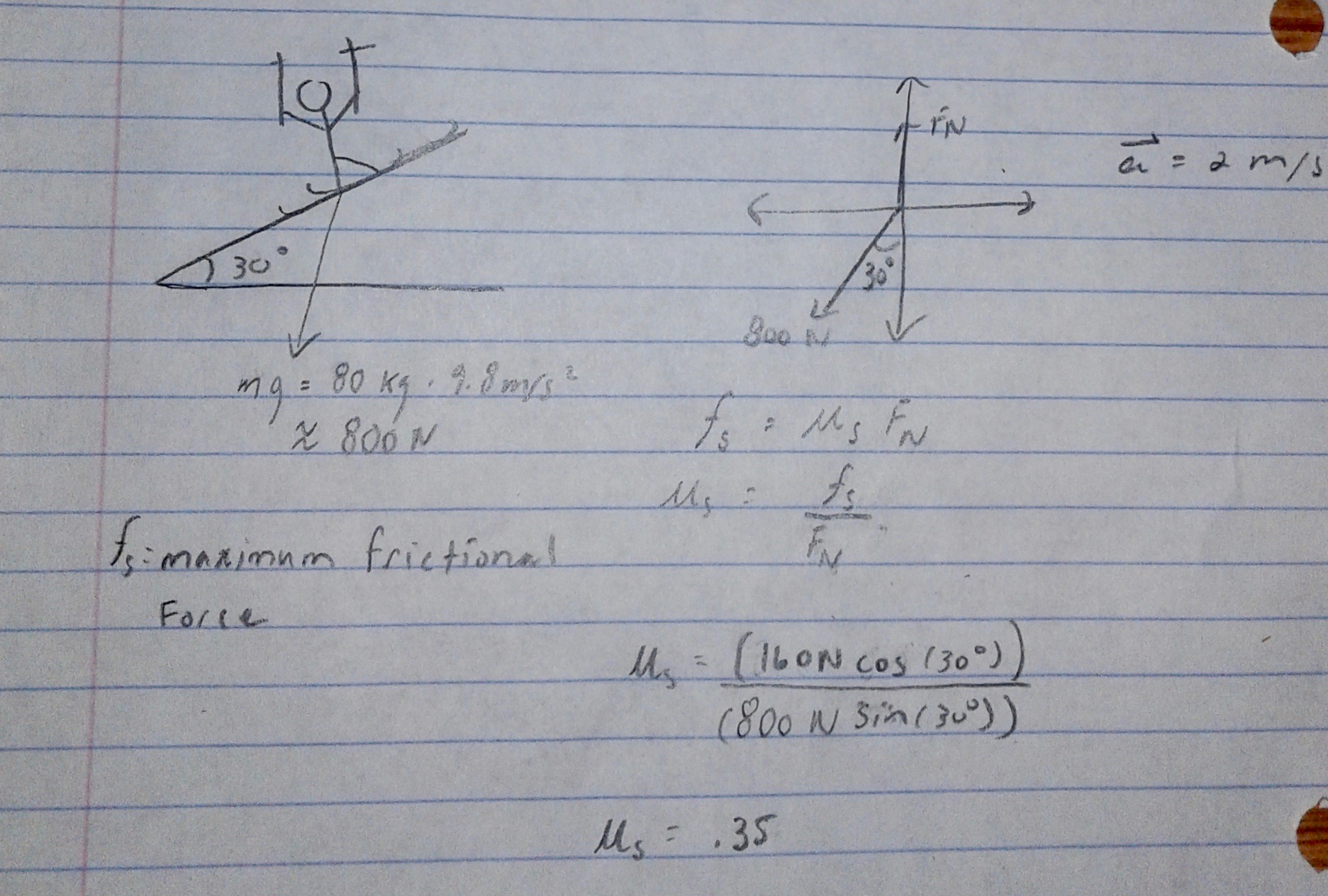
As illustrated, the coefficient of static friction of Joe's ski skins would be .35. This can then be used to calculate how steep of a slope Joe can ski so long as he know his mass using the equation:
theta=arccos(mgu)
*u is coefficient of friction
These same features also make glaciers prime for ski touring. Ski touring is when you have a special binding that allows your ski boot to have a free heel and pivot on the toe. A type of "skin" is then put on the base with an adhesive. The skins have small hairs on the bottom that allow the ski to be easily pushed in the forward direction, but not the backwards direction. Skis like this are most popularly used to access ski areas that lack a lift, but they are also necessary for any ski mountaineering. They are very similar to a snowshoe, but the forward glide and dual purpose make them much more practical. You can think of the Kahlitna Glacier as the highway and the skis as your vehicle for access the peaks in the Denali area.

Image Courtesy of backcountry.com
Physics
The first question many people ask
when they first hear about this ski touring method is,
"How steep can they go?" The short answer is that it
varies based on skin brand and use, but it can more or
less be figured out with physics.The first step is to figure out the coefficient of friction of your ski skin. The easiest way to do that is to find a slope with a known angle and bring a pack and various weights at a constant acceleration. You then go up the hill with increasing weight until the skins no longer provide sufficient friction (You slip). The calculation would be fairly straight forward. Lets assume Joe wanted to try this in his back yard where there is a 30 degree hill. He finds that his skins no longer can hold his weight on the slope when he has a total mass of 80 kg with his pack when he accelerates at 2 m/s^2.

As illustrated, the coefficient of static friction of Joe's ski skins would be .35. This can then be used to calculate how steep of a slope Joe can ski so long as he know his mass using the equation:
theta=arccos(mgu)
*u is coefficient of friction