The Physics of Self-Arrest
Obviously, the biggest dangers of glacier
travel are crevasses. Disguised by snow bridges and devious
cornices, crevasses are basically bottomless pits of death
formed when the glacier moves over terrain and cracks.
In the event someone falls into a crevasse, it is vital that one or more members of a rope team self arrest. Self arresting is done by using your body, ice axe, and sometimes crampons/skis to slow and eventually stop the person from falling to their death. An illustration can be found below, and more information on the intricacies and different types of arrest for certain scenarios can be found here.

Image courtesy of PBS
This problem can best be solved by assuming that the top-dollar ultra-light mountaineering rope has a negligible weight and no friction with the ice. Under these circumstances, the problem can be looked at in one dimension, as shown below:
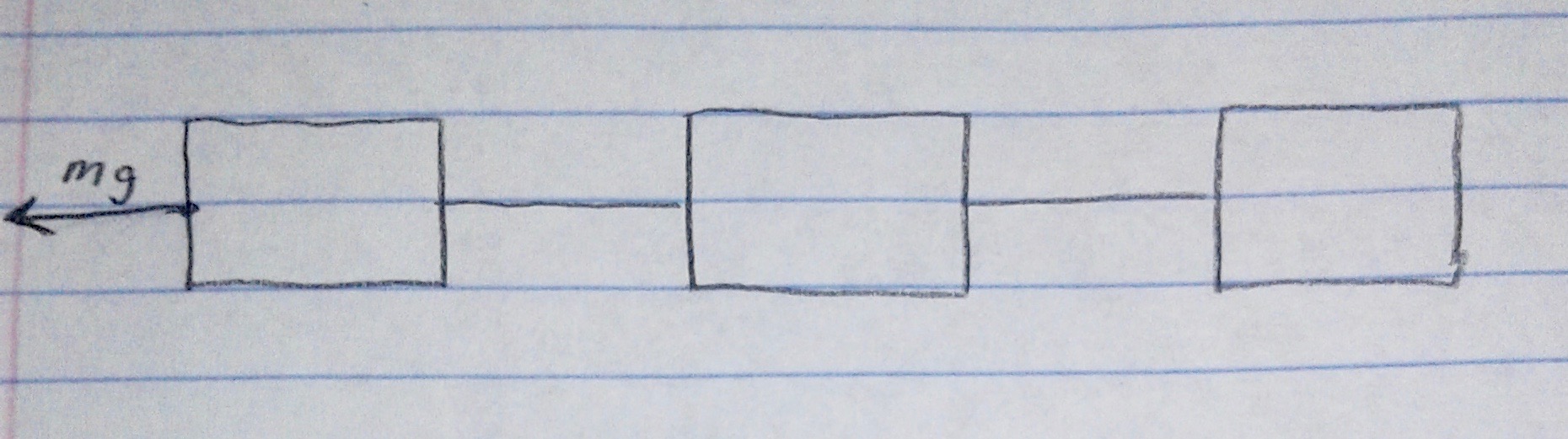
The box on the left represents the fallen climber, while the other two are the climbers in self arrest. The next step is to figure out the tension in each strand. This part can be a bit tricky, so let's say each climber weighs 75kg with all of his gear. It is important to note that only the fallen climber is exerting any tension on the rope
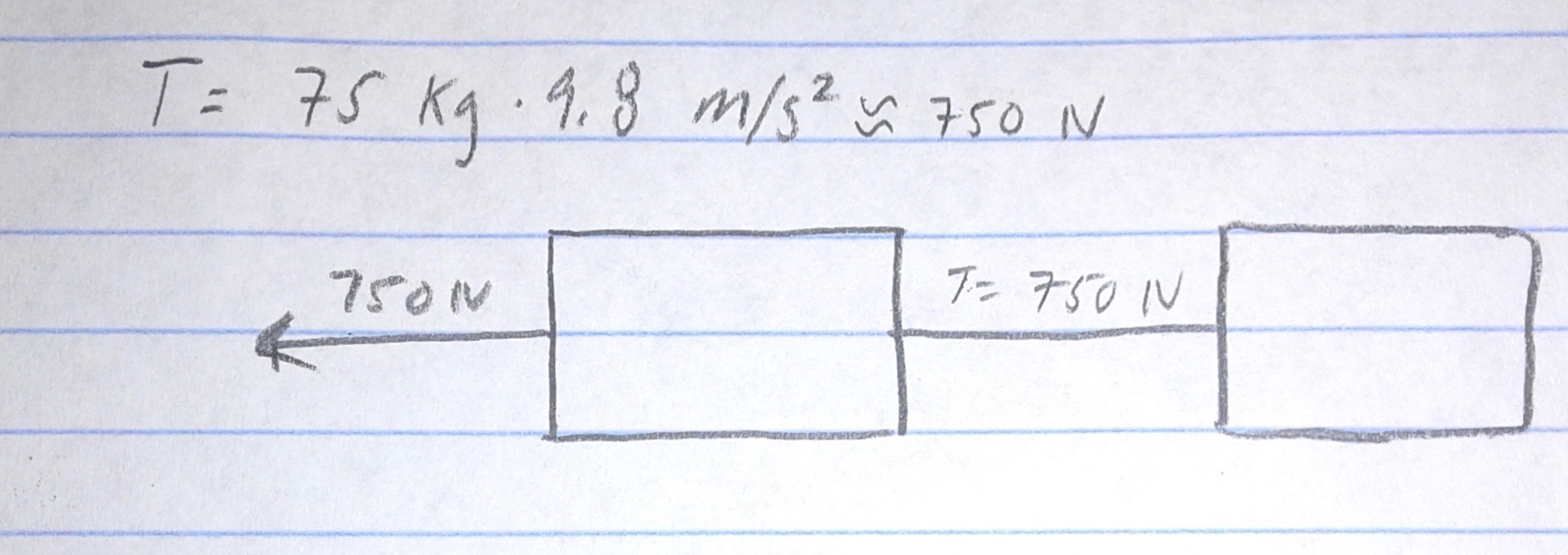
As demonstrated, since there is only one force acting, the tension is going to be the same as long as both the safe climbers self arrested properly. From this we can deduct that since neither the left nor the right climber are bearing more weight, it would be easiest for the right climber to unhook from the rope since he only has it on one side of him. After that he can begin building an anchor to safely pull the fallen climber from the crevasse.
It is important to note that this is a very basic example, and that either climber can begin building the anchor, and it often times comes down to who has the most experience.
In the event someone falls into a crevasse, it is vital that one or more members of a rope team self arrest. Self arresting is done by using your body, ice axe, and sometimes crampons/skis to slow and eventually stop the person from falling to their death. An illustration can be found below, and more information on the intricacies and different types of arrest for certain scenarios can be found here.

Image courtesy of PBS
Physics
Once the self arrest is completed, the next
problem arises. A Z-pulley needs to be built so the victim can
eventually be pulled out of the crevasse. Looking at the image
above, which strand of rope would have the least tension in
it? Which climber, the one on the left or the one on the
right, would most easily be able to end their self arrest and
build an anchor? This problem can best be solved by assuming that the top-dollar ultra-light mountaineering rope has a negligible weight and no friction with the ice. Under these circumstances, the problem can be looked at in one dimension, as shown below:

The box on the left represents the fallen climber, while the other two are the climbers in self arrest. The next step is to figure out the tension in each strand. This part can be a bit tricky, so let's say each climber weighs 75kg with all of his gear. It is important to note that only the fallen climber is exerting any tension on the rope

As demonstrated, since there is only one force acting, the tension is going to be the same as long as both the safe climbers self arrested properly. From this we can deduct that since neither the left nor the right climber are bearing more weight, it would be easiest for the right climber to unhook from the rope since he only has it on one side of him. After that he can begin building an anchor to safely pull the fallen climber from the crevasse.
It is important to note that this is a very basic example, and that either climber can begin building the anchor, and it often times comes down to who has the most experience.