Robotic Arms, Theory Kinematics
 The study of how forces interact with an object is called statics, kinematics is the
mathematics of how an objects moves. There is forward and inverse kinematics. Forward kinematics
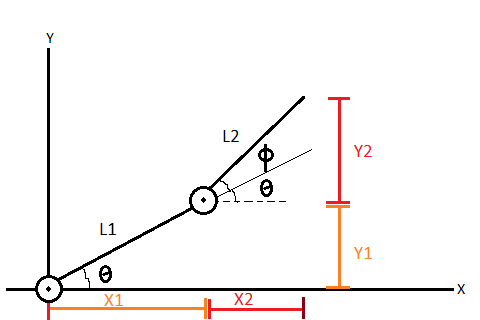
is trying to find the x and y position of the robot arm when given the angle of rotation, Θ and
Φ which are the angle of rotation for each motor. Forward kinematics is much easier to derive and calculate than inverse kinematics but is less
useful for real world applications.
The study of how forces interact with an object is called statics, kinematics is the
mathematics of how an objects moves. There is forward and inverse kinematics. Forward kinematics
is trying to find the x and y position of the robot arm when given the angle of rotation, Θ and
Φ which are the angle of rotation for each motor. Forward kinematics is much easier to derive and calculate than inverse kinematics but is less
useful for real world applications.
First we will find:
x1 = L1*cos(Θ);
y1 = L1*sin(Θ);
Next we find:
x2 = L2*cos(Φ);
y2 = L2*sin(Φ);
Adding these gives us the final x and y position:
x = L1*cos(Θ) + L2*cos(Φ);
y = L1*sin(Θ) + L2*sin(Φ);
With these equations we can determine, given Θ and Φ, the position of the robot arm at its tip.
This is great if we know the rotation of the robot arm and want to find its position but what if we want to work from a position and find an angle?
We need to know what angle to turn the motors to. This is
inverse kinematics.
Inverse kinematics is a much more difficult mathematics to understand. It typically involves Jacobains to
solve a system of equations. Even with linear algebra at our disposal(something I don't have in my tool
belt), the equations to determine Θ and Φ are long and complicated. We will be using a geometric
approach that has already been solved by Serdar Kucuk and Zafer Bingul.
There are two solutions for each equation:
Φ = arctan 2*[ ± sqrt(1-A2) , A ]
Θ = arctan 2*[ ± sqrt(1-B) , B ]
Where:
A = (x2+y2-L12+L22)/(2*L1*L2)
B = (x(L1+L2*cos Φ)+y*L2*sin Φ)/(x2+y2)
As you can see the solutions for inverse kinematics equations are long and complicated. That is why, when designing robotic arms, the DOF should be kept as small as possible as not to complicate the robot. Not only can the equations have multiple solutions, an equation could have an infinite number of solutions or no solutions. Along with the multitude of solutions there are many ways of getting from point A to point B. Do you want a direct path? Do you want the fastest path? Or do you want the path that uses the least amount of energy? All of these constraints add to the complexity of robotic kinematics.