Molecular viscosity, which plays the role of "internal friction" of a fluid, is ultimately the sink of kinetic energy, removing it from the system by thermalizing it. This viscosity, however, only acts significantly a very small scale [3]. As in the NSE, we use $\nu$ to denote the kinematic viscosity. In relation to the molecular viscosity, $\mu$, is $\nu=\mu/\rho$ where $\rho$ is the fluid density.
As mentioned, turbulence consists of a heirarchy of eddies which can be sorted according to size. To resolve the turbulence from the background flow, the flow $\mathbf{u}$ is partitioned as $\mathbf{u}(x,t)=\overline{\mathbf{u}}(x,t)+\mathbf{u}\!'(x,t)$ where $\mathbf{u'}$ is the turbulent component of the motion.
Since motion exists at multiple spatial scales, one can investigate a local Reynolds number of $\mathbf{u'}$ by $Re(l)=u(l)l/\nu$ where $u(l)$ is a characteristic velocity at length-scale $l$. In this way, one can also define the characteristic timescale $\tau(l)=l/u(l)$ over which that motion persists [8]. These characteristic scales can also be defined via harmonic investigation of the NSE using Fourier methods [6].
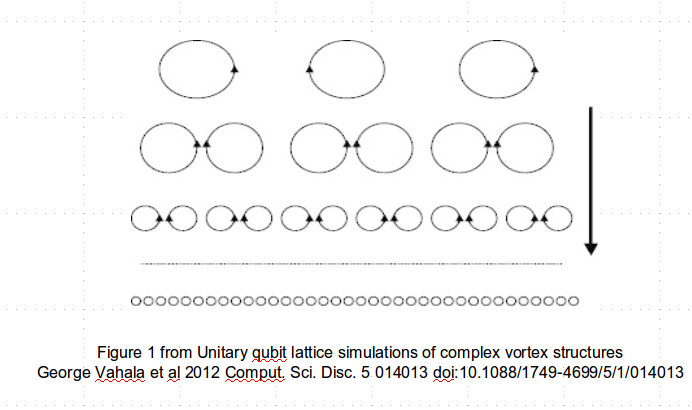
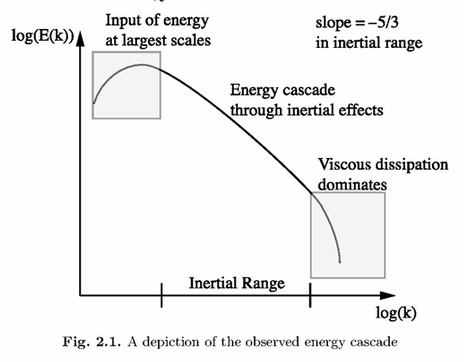
A fundamental mechanism that 'breaks-down' large eddies and transfers their energy into eddies of progressively smaller scales is called the Turbulent Energy Cascade (TEC). The TEC theory summarily says that the (initial or generated) large-scale vortices are unstable and transfer into smaller and smaller vortices until they reach a critical length-scale at and below which the molecular viscosity efficiently thermalized the kinetic energy. Thus, the energy input into the NSE system by the forces $\mathbf{f}$ generate a background flow AND large instabilities. Those instabilities "cascade" until they enter a small enough scale where friction removes their energy, as below in the cartoon schematic.
http://iopscience.iop.org/1749-4699/5/1/014013/article"

In terms of physics, the natural way to examine this phenomenon is in Fourier space using wave-numbers $k$ to quantify spatial scales. Kolmogorov is credited with identifying the scale length $k_\nu=(\epsilon/\nu^3)^{1/4}$ at which the molecular dissipation of energy becomes significant and viscosity can efficiently removes kinetic energy [8]. Here, the symbol $\epsilon$ is used to quantify the rate of energy dissipation per unit mass and is related to vorticity, or more properly, to enstrophy [8]. The cascade can also be presented in the following form, as shown in [1,3,8]:
Figure from Berselli, page45
where the energy $E(k)$ at wavenumber $k$is shown to decrease from the large-scale input through the inertial range. The dissipation scale $k_\nu$ corresponds to the second tick-mark on the horizontal axis.
To illuminate the role of vorticity conservation in the cascade, Guermond et al. [ref. 5] put forth the following analogy. The background flow often changes one of the spatial dimensions of a turbulent feature. Since the fluid is incompressible, the other dimensions must compensate. If the background flow happens to stretch the eddy in the same direction as its curl, the length scale of the other dimensions must decrease [2] and the eddy becomes a smaller eddy. The increased curl of the elongated eddy means that the velocity gradient changes much more quickly, thus increasing its energy dissipation rate [8].