
 |
| The Ideal Gas
Law: PV = nRT |
| The Ideal
Gas Law is a combination: Boyle's Law (P1V1=P2V2) Gay Lussac's Law (P1/T1=P2/T2) Charle's Law (V1/T1=V2/T2) Avogadro's Law (V1/N1=V2/N2 at constant P and T. V/N is expressed as a constant. (Bauer). Combining these equations yields PV = nRT, which can be extremely useful in approximating the behavior of a gas. The equation is for an ideal gas, where the air inside of a tire is definitely not an ideal gas. Still, the ideal gas law is an excellent tool to approximate the behavior of a tire in different weather conditions. P = Pressure, V = Volume, n = Number of moles (or amount of air in our case), R is ideal gas constant (8.314471(15)J/(Mol K), T = Temperature. With this information, we can see what happens to a tire as temperature changes. Image taken from porsche experiment. |
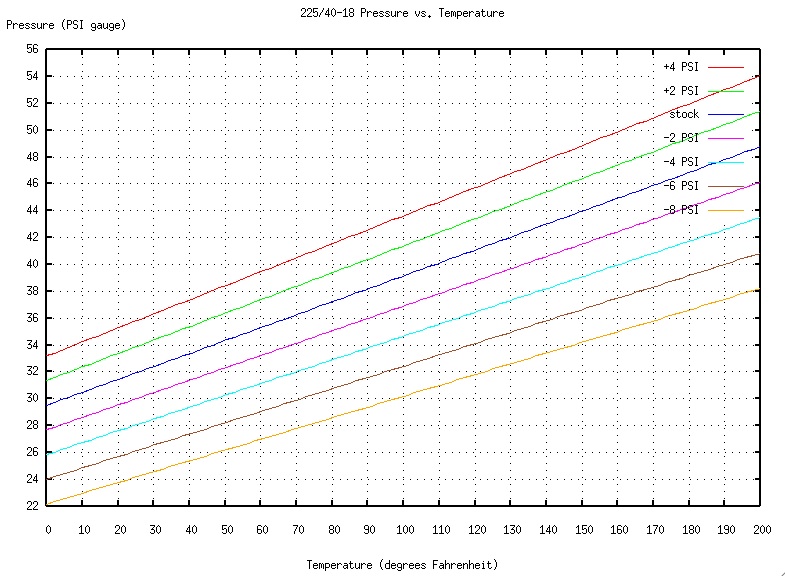 |
| Looking at
the PV=nRT equation,
we see that pressure is directly
proportional to temperature at a constant volume V and n number of
moles. Using the equation, with all other things held constant (the
amount of air in a tire is constant), we see
that as temperature decreases so does pressure. As temperature
increases, pressure will increase. The graph above shows an
experiment conducted by a driver of a Porsche C4 911 when preparing for
a track day, and what temperature would do to his front tires if
temperature varied on the day of racing. An average rule of thumb is
that for every ten degree drop in temperature, tire pressure will drop
by about 1 PSI (Allen). Bear in mind as well that P of the ideal
gas law
equation is the absolute pressure, and not the gauge pressure. Changing
between gauge pressure and absolute pressure, all that must be done is
adding gauge pressure with the atmospheric pressure at the location. |
| Home |
Tire
Environment |
Materials
and Design |
PV=nRT
Behavior |
Behavioral
Consequences |
Tire Summary |
Bibliography |