Broomball By Jonathan The-Daring McMahon

Image courtesy: ChromAnomaly

In broomball, spin is everything. Players don’t “stab” the ball; they smack the living daylights out of it… A good swing results in a good smack of the ball which will make it fly across the ice.

 
Image courtesy: Broomball Wizards

Anything with a “spin” means rotational motion. And everyone knows rotational motion is boss.

Rotational motion is what let’s bicycle tires roll, windmills turn, and the human arm to move in socket. Velocity, as known in the physics world, is a vector. This means that it has both a direction and magnitude. For instance, a ball travels East at 55 meters per second. When directions change new vectors are formed. In a circle, for instance, there are infinitely many vectors that could be formed by making a single rotation. To sidestep all that nonsense when describing things traveling in a uniform circular path, rotational motion takes the stage.

Instead of describing things in terms of unit lengths per time, rotational quantities make use of radians traveled for a given time interval. An example of this is a bicycle tire: if it takes 10 seconds for the tire to make 5 complete rotations (remember that there are exactly 2π radians in one rotation) then the angular velocity is 10π radians per 10 seconds, or π radians a second. Essentially, angular velocity tracks how long it takes something to move part way around a circle. If that “something” isn’t kept on its circular path it will move off directly tangent to the circle in the direction of the applied force.

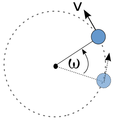     (Note: Angular velocity is often denoted by "w")
Image courtesy: Wikipedia Commons

The beauty of this all is that it is possible to switch between angular and regular (called “linear”) measurements.

This is the standard equation to change between angular and linear velocities:

(Angular velocity) x (Radius from axis) = Linear velocity

When the radius increases, so does the linear velocity. This is probably something which is already obvious. If you have ever ridden in a big truck you know that changing out smaller tires for large ones completely throws off a vehicle’s speed gauge. This is directly associated with the angular velocity equation. This is why broomball sticks are awesome!

Out there on the ice, holding the stick like a champion gladiator, the player is the axis is the axis of rotation. Arm and stick length combined results in the system’s radius. The longer the radius, the faster the end of the stick moves through space tangent to the circular path. A fast swing and a long radius mean incredible results! 

 
Image courtesy: Chris Rooney