Untitled Document

Running with Pendulums

Understanding simple pendulums is important because arms act as alternately swinging pendulums when running. The period (T) of a pendulum (arm) swing is the time it takes for the object to oscillate back and forth once. The amount of time for the arm swing period depends ONLY on the arm or pendulum’s length. This speed has no mass dependence as shown in the following free body diagram derivation.

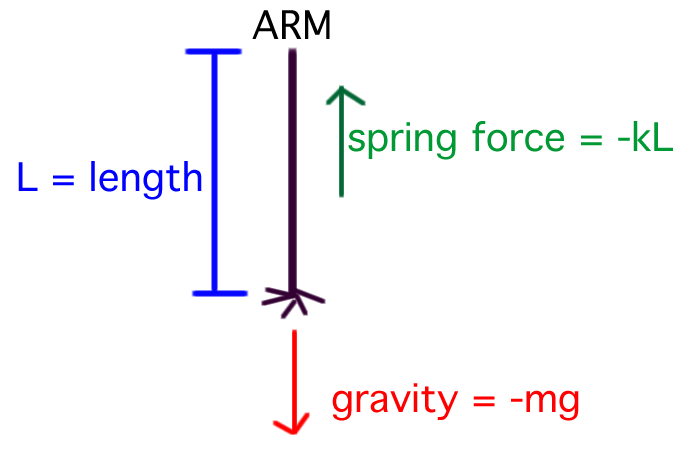
Looking at the sum of the forces on this arm’s free body diagram, we see that the force of the arm is equal to the force of gravity.

Fs = Fg

We can use the spring force from Hooke’s Law because the runner’s arm represents a physical system for which the force varies with position. From this, we can substitute in values and find k (spring constant).

-kL = -mg
k = mg / L

where L is the length of the arm or pendulum; g is acceleration due to gravity; and m is the mass of the hand and arm.

Also from Hooke’s Law, we know that angular frequency (w) measures how fast an oscillation occurs and that w = {[k/m]}**

Since we know k, we can substitute it in the find w:

w = {[k/m]} = {[mg/Lm]} = {[g/L]}

Finally, the period of the runner’s arm (T) is found using the equation and representation of w:

T = 2µ***/w = 2µ / ({[g/L]})
T = 2µ {(L/g)}

Seeing from this equation, the only variable to determine T is L. NO mass dependence.

This derivation was to show that, no matter how heavy a runner’s arms are or what they are carrying, with shorter lengths of arms cause the arm to swing faster. Thus, the arm swings faster which causes the runner to run faster. Shortening the arms can easily be done by bending at the elbow with a 90-degree angle or less.

This is useful for efficient running because the runner uses less muscle energy to move the arms. The runner can actually relax the arms and let the arm swing happen naturally with the bend.

**{ } means taking the square root of what is inside the brackets

***µ is pi = 3.14........