Engineers would love a soft, malleable, ferromagnetic superconductor impervious to impurities or applied current and magnetic fields. Naturally, though, this isn't the case. Superconductors do hold amazing potential for practical applications, but there are a lot of properties that must be considered.
Critical Magnetic Field and Current Density
We have already discussed that a superconductor must be cooled to a certain temperature to lose its resistance. However, this is not the end of the story- a material can be driven out of its superconducting phase by conditions other than temperature. One of these is a magnetic field. One of the most popular properties of superconductors is that it is a perfect diamagnet- it allows no magnetic field to penetrate it (The Meissner Effect). This is displayed by the popular pictures of permanent magnets hovering above superconductors.
You can imagine the Meissner effect by applying a magnetic field to a superconductor already below its critical temperature. The changing flux of applying a magnetic field induces a current and therefore a magnetic field that opposes the original field. In a normal conductor these induced eddy currents die out because of the conductor's resistance once the magnetic field stabilizes. In a superconductor, however, these eddy currents persist because there is no internal resistance. Hence, the opposing magnetic field persists, and does not allow the external field to penetrate the superconductor.
Now, imagine a superconductor above its critical temperature- in its normal state. Now, apply a magnetic field to it, and lower its temperature until it reaches its superconductive state. What happens to the magnetic field inside the superconductor? For many materials, if you changed its temperature and applied field in this order, the magnetic field would simply persist inside the material- there is no reason that a magnetic field could not remain inside. However, the superconductor allows eddy currents to flow indefinitely, and the magnetic field is again expelled. [As explained earlier, this picture is only this simple for Type I superconductors- Type II can have a mixed phase, and allow magnetic fields to penetrate superficially].
Driving this magnetic field outside the superconductor, of course, requires energy, so if a sufficiently strong magnetic field were applied and required a sufficient amount of energy, the material would instead be driven out of its superconducting phase. This 'sufficiently strong' magnetic field is called the Critical Field: Bc. Again, Type I superconductors have a single critical field that will cause them to change phase, while Type II have a lower and upper limit; between which they are in the mixed phase.
The phase is also determined by the current through the cross sectional are of the superconductor- the current density. If current is driven through the sample above the critical current density Jc, the material retreats to a normal resistive state.
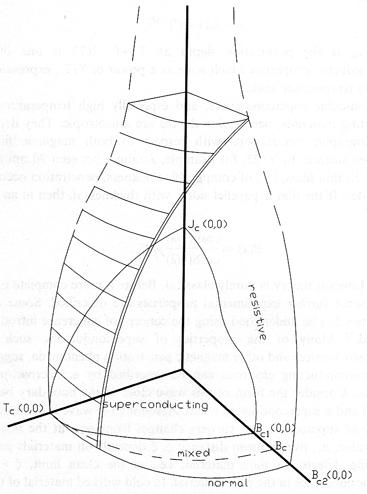
The Critical Temperature, Critical Magnetic Field, and Critical Current density are all inter-related. A phase diagram for an arbitrary sample is shown below. The notation Tc(0,0) indicates that that point is the critical temperature when B and J are zero. Notice that because of the mixed state, this represents a Type II superconductor.
(Bourdillon p. 17)