INTRO BACKGROUND BALLET  BALLET PART 2 BREAK DANCING   BIBLIOGRAPHY

background photo:http://www.photoworkshop.com/artman/publish/lois_greenfield.shtml/ Louis greinfeild

The physics of a ballet poses
Have you ever wondered how ballerinas keep themselves from falling over?
The center of gravity and Newton's third law explain their ability to keep their bodies
upright in such graceful positions.

  pose 

http://www.peterwerner.net/dance.html


Ballet poses depend heavily on the “center of gravity”. Dancers must maintain balance by aligning their center of gravity directly above the line passing through the area of support on the ground.  Their net force and torque must equal zero in order for the dancer to maintain the position firmly.  


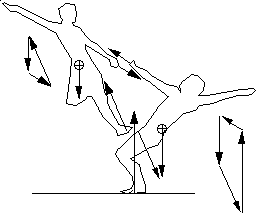
 part2of2                 pose 2

photos from:

http://www.peterwerner.net/dance.html


Sandra Brown and Johann Renvall (ABT) in Airs, photo by Nancy Ellison

The black and white photo with the arrows shows   the center of gravity of both dancers (represented by the little circle). The arrow that is pointing downward from the center for gravity show's the direction of the force. The arrow pointing upward from the ground is the floor acting on the dancers.  The sum of the forces is equal to zero, therefore the torque is zero.

Newton's third law states that for every action, there is an equal but opposite reaction. This is seen in the photo. The idea of the force of gravity pushing vertically on downward on the , and the force of the ground pushing upward on that same vertical line shows newton's third law. It is also seen between to two dancers. Dancer one exerts force on dancer two, but since the forces are the same, but opposite, the net force is still equal to zero. we also see that the dancer has the ability to control the area of which he or she places their foot to adjust the center of gravity.

     

turns

http://insaniescreed.tumblr.com/post/63535880934


figure 1
The basics of the speed of turns

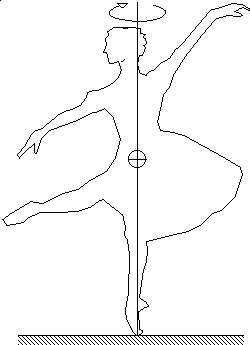photo

http://www.peterwerner.net/dance.html

figure 2
Not only must dancers maintain balance while being stationary, but dancers must also maintain balance while turning. Dancers must
learn to control how fast they turn, and for how long.

here are somethings to remember before we continue.
  • L=angular momentum, I=rotational inertia, w=angular velocity, and T=torque , which is the change in angular velocity and time
  • when our L is constant, there is no torque
  • L=Iw
  • (delta)L=(T)x(delta)time

I is basically the measurement of the level of difficulty it takes or something to start moving. So when finding I, we must take to account the mass
of the dancer.  The grater the mass, the larger an object's inertia is.  And when I is larger, the spin rate is smaller. Inertia is also dependent on the radius of an object.
In a dancer's case, while she is spinning, placing the foot to the knee and twisting the leg out will decrease the dancers speed. This is because inertia gets larger, causing angular velocity to slow down. If the dancer, pulls her leg inward, she will spin faster. (refer to the clip above, figure 1)

The torque needed to begin the turn can be exerted against the floor by two feet with a distance d. simply speaking, when pushing off the ground, the ground pushes back, allowing the dancer to spin.