|
Physics of a Jumperoo™ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Using Newton’s second law, 
, we can multiply each side by mass
in order to achieve this handy formula 
We don’t know the acceleration of
the ball or the spring at these points, although they can be found, we are
going to relate this experiment in terms of velocity
and s-axis.
By knowing that a rate is
measureable, in example kilometers per hour [km/h], we can say that 
,
or velocity of the ball in relation to the spring is the total change in
position of the ball (compressed to restored) divided by the time it takes to
leave the spring (measured as [m]/[s]).
Acceleration is measured as the rate of change of the velocity or
.
Substituting this into the equation
,
this become 
.
https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcR0IKFnJiKN7K0zZfEaWf2FKuFXWCm2xg3SrG69r1tgXu-M8qpGNA
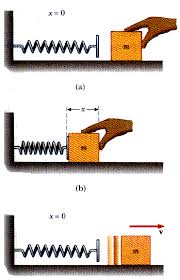
The position of the spring
undergoes some displacement from its natural position when the ball is pushed
onto it. We can establish the arbitrary
s – axis as having and origin starting at the point s. The spring displaces to
a point at its natural resting position length s, to a point here 
,
and also to the point of need compression here, 
,
as being less than that of the position of s, is now negative due to
compression (see what I mean about arbitrary s-axis) and so 
The velocity at the point that the
spring is compressed to 
is when the velocity is at a minimum, 
.
The velocity at the point 
,
when the ball leaves the spring is at is maximum so we will call this velocity,
.
With these values 
.
Any time that we will look at will be from the point the spring is released until
it is restored and this will be from 
until 
,
and then 
measured in seconds
[s].
Using these relationships
mass, and 
[kg] and 
[s], we can state this, 
,
so 
,
and [N] = [N]. Now it is east see that 
.
This analysis
shows that the Force that spring used in launching the ball is equal to the
Force that the spring had due to the change in position of the s-axis. It also
shows that the force of the spring 
is the opposite in direction than change in
position ∆s, denoted by its sign convention.
Is Energy conserved?
|
|
|
|
|
Uaf Physics 211X |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|