Projectile Motion
Galileo was the first person to understand projectile motion. He realized that the motion of an object depended upon two motions. Before his time, people believed a thing called “impetus theory.” That is, an object followed a straight line until it lost its impetus, at which point the object began falling to the ground. However, a closer observation on Galileo’s part proved that theory wrong. He discovered that objects follow a curved path [5].
Projectile motion follows two motions: the
motion of gravity on
the object and the distance the
object travels. Recall that the equation for projectile
motion is
|
xf = |
where xf
and x0
are the final and initial displacement (respectively), v0
is the initial velocity, a is acceleration,
and Δt is the change in
time. If we were to graph
an equation of the form, with Δt
and xf
as the variables, we would get a graph that would look like
this:
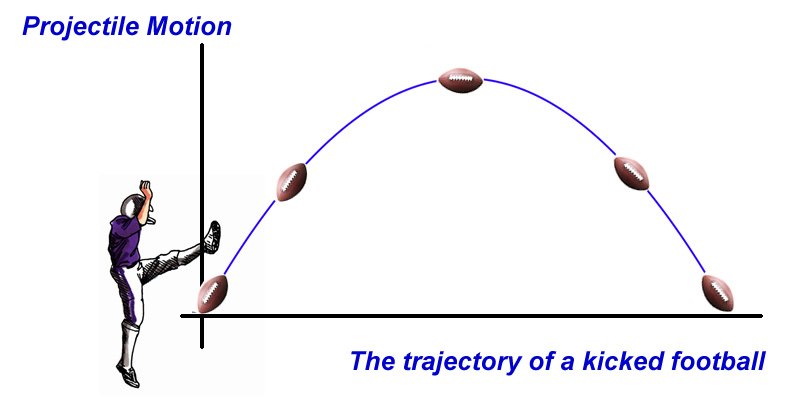
As you can see, the graph above looks like a parabola. This is assuming the acceleration of an object is constant [5]. By definition, the jerk of an object is equivalent to the change in acceleration over time. If acceleration wasn't constant, the equation for an object in motion would look like this:
|
xf = |
x0 + v0Δt + ˝a0Δt2 + ⅙jΔt3 |
where j is the jerk. As you can
see this equation looks like a cubic function. This equation
gives a more accurate description of projectile motion,
compared to making acceleration a constant. However, the
change in acceleration of an object in motion is often so
small that the jerk is often neglected. The gravity of the
Earth acting on an object barely changes from one altitude
to another. This is why we often describe projectile motion
as a parabola [1].