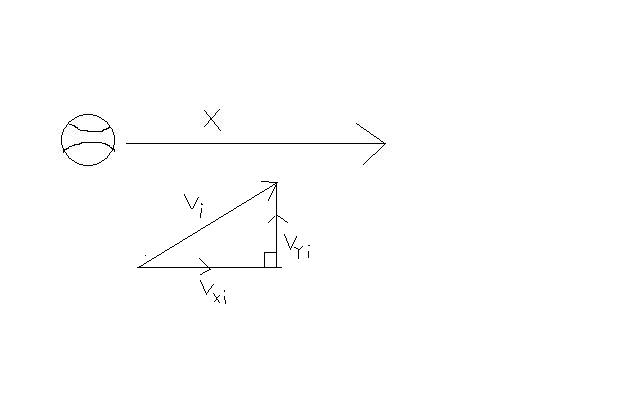
The ball in motion- parabolic break down     Problem: Find the minimum force it takes to throw a baseball from the center field of wrigley field to home plate where a catcher will receive the ball at the same height that the ball was released from the outfielder's hand, a distance of 400 ft (123 m).  The angle of trajectory that an object will travel the farthest when released, ignoring wind, is 45o off the horizontal ground. The mass of an official MLB baseball is between 5 and 5 1/4 ounces so we will use a 5 1/4 ounce baseball (0.1488kg) since it is be the largest mass allowed by the MLB.  Remember the gravity of the earth accelerates objects at a rate of 9.81 m/sec^2.  The arm span of the man throwing the ball is 8 ft (2.4 m)     There are two important parts to figuring this problem out.  First finding the velocity at which the ball was released and then using the man's arm span and the value for the velocity found in the first part to find the acceleration of the ball while in the mans possession this value times the mass of the ball will give rise to the minimum force required for this man to throw a ball to home plate.                          Step 1: The X-component                                                                Work (from picture, vxi = vi * cos (45)  ) xf = xi + vxi * deltat + ½ * ax * deltat2 xf = 0 + vxi * deltat + ½ * (0) * deltat2 xf =  vxi * deltat xf  = vi * cos (45) *  deltat                         Step 1: The Y-component Work (from picture, vyi = vi * sin (45) ) yf = yi + vyi * deltat + ½ * ay * deltat2 0 = 0 + vyi * deltat + ½ * ay * deltat2 0 = vi * sin (45) * deltat + ½ * ay * deltat2 Step 1: Manipulate and Combine x-component and y-component x:    xf  = vi * cos (45) *  deltat                                                                                                                    manipulate :                                                                                                                                                                                              1. 0 = tan (45) * xf  + ½ * ay * xf2 / [vi2 * cos2 (45)] y:    0 = vi * sin (45) * deltat + ½ * ay * deltat2                                                                                         2. -tan(45) * xf  = ½ * ay * xf2 / [vi2 * cos2 (45)]                                                                                                                                                                   3. -2 tan(45) * xf  / ay = xf2 / [vi2 * cos2 (45)] x: deltat = xf / [vi * cos (45)]                                                                                                                    4.   vi2 * cos2 (45) = -ay * xf /[ 2tan(45)]                                                                                  5.  vi2  = -ay * xf /[ 2tan(45) * cos2 (45)] x into y: 0 = vi * sin (45) * xf / [vi * cos (45)] + ½ * ay * [xf / (vi * cos (45))]2                                             6.  vi = squrt(-ay * xf /[ 2tan(45) * cos2 (45)] )                                                                                                                                                                             vi is about 52 mph Step 2: Finding the force.       At this point in the problem we have solved for the initial velocity of the ball when it leaves the outfielders hand.  Now in order to find the force the man exerted on the ball we must find the magnitude of the balls acceleration while in his possession.  We need this because F = ma and we know the mass because it is given.  To find the acceleration you can use one of the equations provided on the previous link.  It will be labeled clearly below where, vo ,stands for velocity initial. equation: vf2 = vo2 + 2a deltax a =   (vf2 - vo2) / ( 2 deltax )  known values:                                                                                                    Plug in known values to find (a): vf = squrt(-ay * xf /[ 2tan(45) * cos2 (45)] )                                                         vo = 0 m/sec                                                                                                       a =   (-ay * xf /[ 2tan(45) * cos2 (45)] - 0) / ( 2 deltax ) deltax = 8.ft = 2.4m                                                                                           m = 0.1488kg                                                                                                     a = [9.81 * 123 /( 2tan(45) * cos2 (45)) ] / ( 2 * 2.4 ) ay = -9.81 m/sec^2                                                                                                xf = 400. ft = 123 m                                                                                            a = 251.38  = 250 m/sec^2 Plug in values to find force (F): F = ma F = (.1288) (251.38) = 32.38 = 32 kg*m/sec^2 = 32 Newtons = 32 N Conclusion: The minimum force required for this man to throw the baseball is 32 N which will accelerate the ball 250 m/sec^2 and will cause the ball to leave the outfielders hand at about 52 mph.