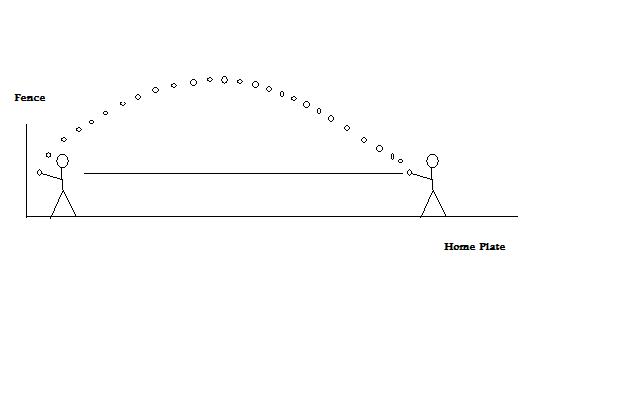
Parabolic Motion- baseball oriented
When a baseball player throws a baseball the ball will follow a parabolic motion. It is easy to see this, first grab a baseball and then throw it upward into the air. Let me guess the ball went up and then came back down either into someone's hands or to the ground. This motion comes about due to the affects of gravity on the baseball. The force of gravity gives the ball, after being released from a hand, acceleration (a) that is approximately 9.81 m/sec^2 in magnitude. The magnitude of gravity's affect on the ball can be found by taking the acceleration value (9.81 m/sec^2) and times it (*) by the mass of the baseball (m). The value of this force is approximately what you would see if you weighed the ball on a bathroom scale, this is because weight is the magnitude of earth's gravitational force acting upon an object. The force (F) is described by Sir Isaac Newton's second law of motion assuming (a) is constant F= m*a, this equation is what helps physicists discribe the parabolic motion of objects including that of the baseball. On the following page you will discover an example and break down of Newtons second law being used to determine the minimum force with which an outfielder must throw a baseball in order to reach home plate from the outfield fence without it hitting the ground.
Force
Equations for translational motion (assuming constant acceleration)
There are a few equations that an individual must be aware of in order to find the minimum force with which an outfielder must throw a baseball for it to reach home plate. These equations are listed below, the derivations of these equations can be found in the textbook University Physics with Modern Physics by W. Bauer, and Gary D. Westfall.
Equations Index for variables
xf = xi + vix * deltat + ½ * ax * deltat2 xf is the final position corresponding to the x-axis
yf = yi + viy * deltat + ½ * ay * deltat2 xi is the initial position corresponding to the x-axis
yf is the final position corresponding to the indicated y-axis
vfx = vix + ax * deltat yi is the initial position corresponding to the indicated y-axis
vfy = viy + ay * deltat viy is the initial velocity in the y direction
vfy is the final velocity in the direction parallel to the y-axis
vfx2 = vix2 + 2 * ax vfx is the final velocity in the direction parallel to the x-axis
vfy2 = viy2 + 2 * ay vix is the initial velocity in the direction of the x-axis
deltat is the change in time