In 1676 Newton amended mathematics by proving that the sum of a series with negative n integers converges, or reaches a certain value when summed to infinity when the absolute value of x is less than 1.  
    Newton also polished the work of his professor Isaac Barrow who was the first Lucasian Professor of Mathematics and Natural Philosophy at Cambridge and came up with what is known as the Fundamental Theorem of Calculus:

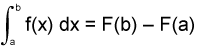
http://archives.math.utk.edu/visual.calculus/4/ftc.9/

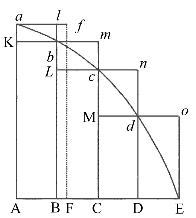
 By adding an infinite amount of diminutive rectangles under any continuous curve with an initial point on the curve a to the final point b being integrated, the difference between two functions F(b)-F(a) is obtained.

http://aleph0.clarku.edu/~djoyce/newton/method.html

    It is important to mention that without the use of the integral and the derivative, it would be much more difficult for physicists and engineers to improve living conditions of society or even come up with luxuries such as televisions, electricity, cars, etc; since calculus is the base for determining the proper function of such creations. 

Back           Forward