Paper Airfoil Aerodynamics6 - Paper Airfoil
Design Characteristics | |
|
I.
A. Next B. Back Designing paper
airfoils presents a number challenges compared to using other
materials. In the words of
one budding paper airfoil designer, "Paper sucks as a building
material". Not only is paper
susceptible to mold and mildew, it is easily compromised by moisture,
fire, and deformation due to high acceleration or rough handling. It is not capable of spanning
great distances without becoming inefficient due to its weight. It is also not capable of
supporting great loads by itself without rapidly becoming too massive or
flimsy to fly. Most paper airfoils do
not have their own means of propulsion, and must be launched by hand. The kinetic energy imparted to the
airfoil by the human hand is relatively small, resulting in low altitudes
attained by the airfoil during flight. Because of this, the goal of a
good gliding airfoil is to decrease the vertical rate of descent enough to
increase time aloft. If the
rate of descent is negative, the airfoil will increase in elevation at the
expense of its own kinetic energy, slowing the airfoil until boundary
layer separation occurs. If
an airfoil's rate of descent is greatly positive, it will quickly lose
altitude but gain kinetic energy and it's time aloft will be quite
low. Therefore it is
desirable to minimize the rate of descent while keeping it positive enough
to prevent a stall. Mathematically, the
rate of descent is dependant upon a number of factors, the velocity of the
airfoil, the coefficient of drag of the airfoil, the density of the fluid,
the wingspan, the span efficiency of the wing (basically how efficient the
wing is in generating drag-producing tip-vortices. A number closer to e=1 would have
very little drag due to this phenomena. Higher aspect ratios give a larger
value to e), the surface area of the airfoil, and the weight of the
airfoil. The physical
equations used to find the minimum speed necessary to remain aloft for an
arbitrary airfoil are displayed in Figure 6.2. Stability during
flight is generally a good thing.
Most aircraft feature vertical and horizontal stabilizers in order
to keep the aircraft flying straight and level. In paper airfoils, it is generally
not necessary to feature tail fins for stability, as the entire airfoil
can provide stability if designed correctly. If a paper airfoil is unstable, it
takes only a relatively small change in airflow to change the flight
characteristics drastically. Every airfoil has at
least two points about which the airfoil will tend to rotate through
during flight. The first is
known as the center of mass.
All objects in flight tend to want to rotate about this point. The other point of rotation is
known as the center of drag.
It is the point about which the airfoil will rotate due to the
forces of drag. Generally, it is desirable to place the center of drag behind the center of mass for small projectiles. This leads to a more stable airfoil and a straighter path of flight. Darts, and paper airplanes use this property to fly true. This can be accomplished by attaching more mass to the front of the airfoil, whether through a paperclip, or simply a fold of paper. Another property of the airfoil leads naturally to stability. Increasing the mass of the airfoil leads to greater stability during flight due to Newton's laws of motion. A greater mass requires a greater acceleration to change its path. Unfortunately, it is impractical to increase the mass of the paper airfoil much more than a few grams due to the generally small force of lift generated by the airfoil during flight. Figure 6.3 displays these two points. Yet another way to
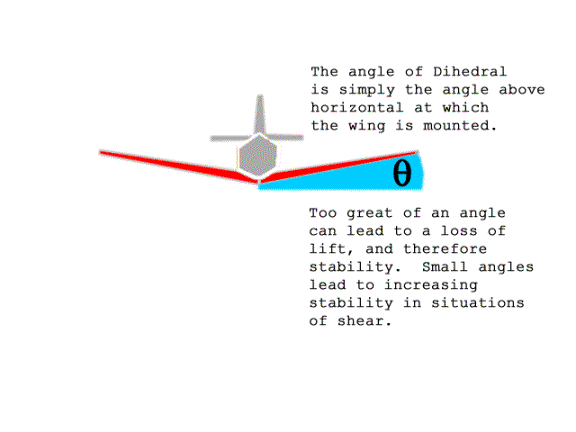
provide stability in unsteady air is to provide a Dihedral angle to the
wings. A Dihedral helps to
prevent rolling when air is flowing at different rates across the two ends
of the airfoil, causing a shear on the airfoil. It has no stabilizing effect when
there is no shear. Figure 6.4
gives an example of Dihedral in a simple airfoil. Listed below are a
number of design tips concerning paper airfoils. . 1.
The angle of attack of
a wing is used to help generate lift. Increasing the angle of attack of
the wing increases the curvature, causing a greater acceleration of
airflow, leading to lower air pressures above the wing by Bernoulli's
principle. Increasing the
angle of attack too greatly results in boundary layer
separation. 2.
The Angle of Dihedral
of a wing provides greater stability as well as marginally better
lift. Birds? wings feature
dihedrals, 747?s feature dihedrals, even paper airfoils feature
dihedrals. The angle of
Dihedral of a wing is simply the measure of what angle the wing is mounted
at above horizontal. 3.
Greater speed results
in an increase in lift.
Indeed, slow moving wings provide very little lift. Large airplanes get around this
fact by increasing their angle of attack through the use of flaps to
change the curvature of the wing.
As it is relatively difficult to adjust the curvature of a paper
airfoil while in flight, the adjustment of flaps beforehand allows the
pilot of a paper airfoil some control over his airfoil's flight
characteristics. 4.
Airfoils with larger
cross-sections suffer greater drag than those of thin airfoils. This is why a fighter-jet's
airfoil is typically thinner in profile than that of a Cessna
aircraft. Although,
typically, increasing the thickness of a wing generally increases its
curvature, leading to greater lift.
For the case of paper airfoils, which are mostly flat, increasing
the curvature of the wing leads to a loss in stability and a very large
increase in drag.
5.
Airfoils with shorter
chord lengths typically suffer from less viscous drag than those of longer
chord lengths. These wings
are called high-aspect ratio wings, The aspect ratio is the ratio of
the wing's wing-span to it's surface area. For paper airfoils, due to lack of
rigidity at long lengths and short chord lengths it is possible for a wing
to fold in on itself at speeds of sustainable flight. This typically puts an upper limit
to a wing's span of only a few tens of centimeters when it is constructed
of paper, and therefore most paper airfoil wings are low-aspect
ratio. I.
A. Next B. Back |
Figure 6.1 ? Aspect Ratio
Figure 6.2 ? Finding the minimum forces of lift, drag, and decent rate for an arbitrary airfoil.
Figure 6.3 Center of Mass and Center of Drag
Figure 6.4 -- Dihedral angle.
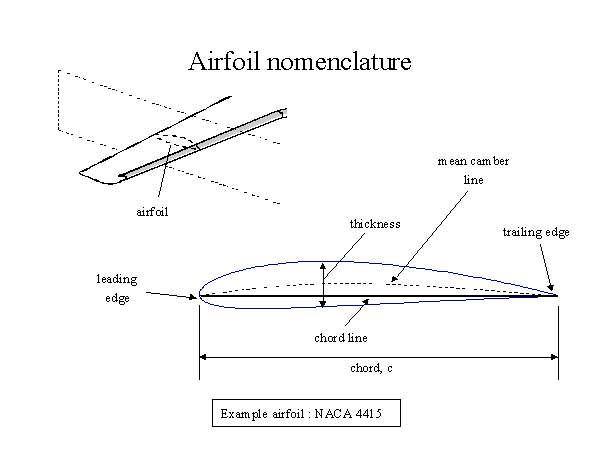
Figure 6.5 -- Airfoil Nomenclature |