Mountain and Lee Waves

Mathematics Intro

The mathematics behind Mountain Waves are often simplified using the Linear Wave Theory. It starts by assuming a steady state, two-dimensional Boussinesq airflow over small amplitude mountains, and that the mountains in question are sinusoidal in shape. Once the linear wave theory of mountain waves is established, it's then expanded upon by adding Nonlinear Terms, and then later considering large-amplitude waves.

This site won't go into the entire derivation for mountain waves, but will instead pick out key points and equations.

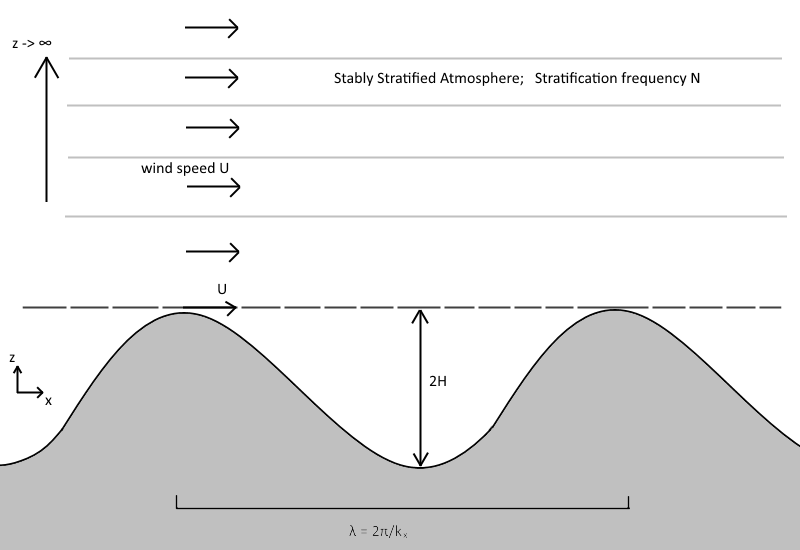
The mathematics will use this diagram for reference.
U is the wind speed blowing over the mountain.
x is the horizontal coordinate and z is the vertical coordinate.
H refers to the height of the mountain.
N is the Brunt-Väisälä frequency or the stratification frequency, which follows the equation:

Where ρ is the density and g is the acceleration due to gravity.