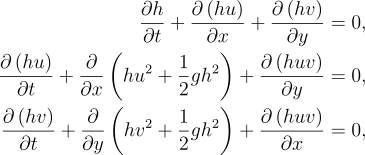Description of Equations

The Shallow Water equations are used for describing the flow of water when the depth is low relative to the wave length. They are derived by integrating the Navier–Stokes equations across the depth. A conservative form of the shallow water equations is shown below where h is the water height, u is the water velocity in the x direction and v is the water velocity in the y direction. The following equations operate on a non rotating plane. 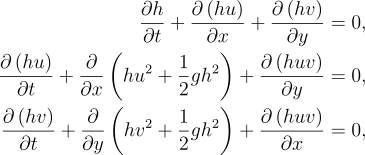The shallow water equations are commonly used to model tsunamis. The shallow water equations are valid for tsunamis because tsunamis are gravitational waves whose wavelength is large relative to the wave depth. Tsunamis are waved generated by a displacement of water often caused by an earthquake or landslide. Tsunamis are very important to understand because they can have a devastating impact on people. For example the Good Friday Earthquake of 1964 not only destroyed Anchorage but a tsunami generated by this earthquake devastated Valdez. The shallow water equations are also useful for modeling erosion because the equations can be applied to modeling of water on uneven surfaces and the water can modify the surface it is flowing on.

Limitations

The shallow water's equations are only valid when the wavelength is large relative to the wave depth and there is no flow along the depth axis. This means that the equations can not correctly simulate phenomenon such as cresting waves or currents that vary with depth because there is no formulation for vertical velocity. Not simulating vertical velocity is a useful property because it simplifies the formulation of the equations and makes simulation computationally easier.