Quantum Mechanics
Basics of Quantum Mechanics
There are two major concepts that play a role in quantum
computing:Uncertainty
The cornerstone of quantum mechanics as it relates to quantum computing is the concept of waveforms. All particles exists as waveforms, or are in Superposition before they are observed. This means that:
1. A wave-function defines their quantitative properties, such as position.
2. This wave-function produces probabilistic values.
This
wave-function will usually be Schrodinger's equation which is:
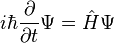
where,
- i is
the usual square root of -1, as the wave phase is
represented using complex numbers. Phase is important
for quantum computing, but not at the level we will be
discussing.
- ħ ("h bar") is just a constant, the Plack constant.
- Ψ ("psi") is the wave itself. The
probability of observing an electron at any given
location is the square magnitude of the wave's
amplitude.
- H, the Hamiltonian, measures how much
energy the particle has.
The key principle for
quantum computing is that, when existing as a wave,
particles, and qubits, live in a space of
probabilities. The probability of being in any one positions
is held in this equation. This is much more information than
in a discrete position, which is why a qubit can be used to
hold additional information when compared to the binary bit.
We should be careful what we call observation; the interaction between any two particles can be enough for the wave-functions of both to collapse into single states. However some theory suggests that this simply entangles the two particles, so that there wave functions are shared; i.e there probabilistic states are described by one wave function. This applies for a human observer as well! Further Reading: Delayed Quantum Eraser
Entanglement
We should be careful what we call observation; the interaction between any two particles can be enough for the wave-functions of both to collapse into single states. However some theory suggests that this simply entangles the two particles, so that there wave functions are shared; i.e there probabilistic states are described by one wave function. This applies for a human observer as well! Further Reading: Delayed Quantum Eraser
Entanglement
Entanglement, as previously mentioned, is when particles
interact, and there corresponding wave functions combine to
form a wave function that the describes the physical system
they compose. With a qubit that will collapse into one of
two states, larger systems of qubits have 2 to the n
total interactions, where n is the number of
qubits.
An interesting facet of entanglement is that it appears to allow information to travel between entangled particles at speeds faster than light. For instance when measuring the spin of two entangled electrons along the same axis spins are always found to be anti-correlated. This means the random outcome of the measurement on this first particle was somehow communicated to the second, so that it can make this patterned choice when measured, despite the fact that measurement causes the wave function to collapse instantaneously, leaving no time for this exchange to occur.
The important thing to remember for quantum computing is that complex systems of possible outcomes when qubits exist in entangled states.
An interesting facet of entanglement is that it appears to allow information to travel between entangled particles at speeds faster than light. For instance when measuring the spin of two entangled electrons along the same axis spins are always found to be anti-correlated. This means the random outcome of the measurement on this first particle was somehow communicated to the second, so that it can make this patterned choice when measured, despite the fact that measurement causes the wave function to collapse instantaneously, leaving no time for this exchange to occur.
The important thing to remember for quantum computing is that complex systems of possible outcomes when qubits exist in entangled states.