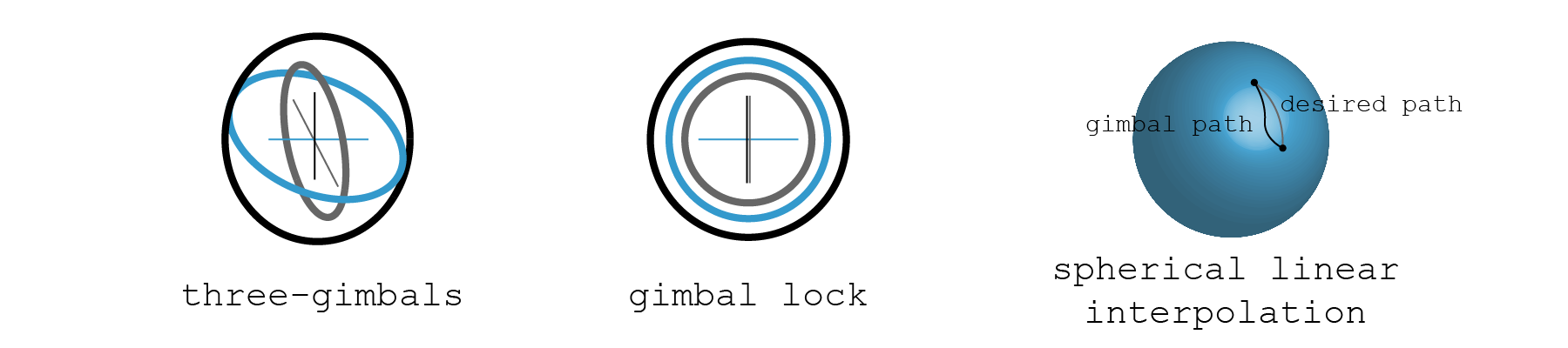
The most useful application of quaternions today is to address the problem of gimbal lock in computer graphics and inertial navigation systems while using Eulerean angles. A gimbal is a pivoted support that allows rotation about a single axis. A three-gimbal mechanism is composed of three individual gimbals working together to acheive three unique axes of rotation. Gimbal lock occurs when at least two of the three gimbals become parallel in the same plane. When this happens a degree of freedom is lost in the mechanism as it temporarily loses a degree of rotation. As a result of this locking, spherical linear interpolation is not possible, e.i. it is not possible to connect two points on the surface of a sphere by a straight line. The gimbal mechanism restricts the path of motion between the two points to that of a nonlinear curve.[5]
Quaternions can represent angles of rotation and motion without the problems of gimbal locking. This is possible as the unit quaternions are mapped to the hypershpere in a four dimensional space. The unit quaternion is represented by q = w + xi2 + yj2 + zk2 and
1 = w2 + x2 + y2 + z2. In this case, the angle of rotation w = cos(theta/2) and vector (x, y, z) represent the point (w, x, y, z). Thus the equation for quaternion interpolation is Q(q0, q1, t) = (q1)(q0-1)t(q0) where t is between 0 and 1 traveling along the linear path of the associated great circle.[6]
