The Physics of Amusement Park Rides Home Page     Roller Coasters     Roller Coasters II     Bumper Cars      Rides That Spin      Bibliography

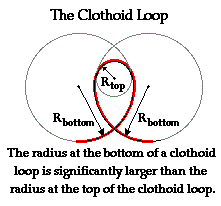
More on Roller Coasters Loops The thrill of hanging upside down traveling in a circle makes the vertical loops one of the funnest parts of the roller coaster ride. If you look closely at modern loops on roller coasters, you will notice that they are not perfectly circular, but they look more like an upside down tear drop. This tear drop shape is called a clothoid loop, which is a shape that has a larger radius of curvature at the bottoms and the sides of the loop and a smaller radius at the top. This is shown in the two pictures below. These vertical loops used to be circular, and were also unsafe. High initial speeds needed to make it around to loop would produce an unsafe amount of normal force felt by the passengers at the bottom, and if the velocity was too small the cars would not make it around the circle.           http://www.cepolina.com/loop%20roller%20coaster%20curve%20yellow.html                 (2 images on the right)  http://www.physicsclassroom.com/class/circles/u6l2b.cfm The advantage of a clothoid loop compared to a circular loop is that they require a lower initial velocity to make it around the loop which results in a lower amount of normal force felt by the passengers. Lets first look at the top of a loop and find the minimum speed needed to go round a loop. In order to go around in a circle, an acceleration  pointing toward the center of the  loop along the radial axis is needed. Ignoring friction, the forces in this direction include the normal force on the car from the contact with the rails, and the force of gravity.  At the top of the loop, both forces are pointing down so the minimum speed is found when gravity is the force causing the change in acceleration and the normal force is zero. At this point on the roller coaster the passengers would feel weightless, however they didn't actually lose any weight, their acceleration is just equal to the gravitational acceleration. So the minimum speed needed to go around a loop is dependent on the radius, so having a smaller radius at the top reduces the minimum speed needed. Now let's look at the bottom of the loop, the normal force is facing up and the force of gravity is facing down. Using Newton's second law of motion we can develop an equation for the normal force.  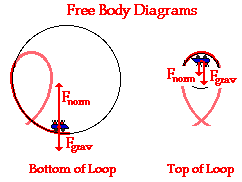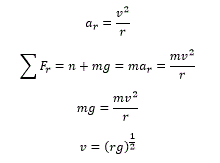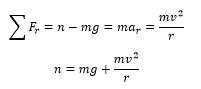It's important to note that the velocity at the bottom will be different than the velocity at the top due to the conservation of energy. Look at the second term for the normal force, if a larger radius is used for the bottom of the loop compared to the radius used for the top, then the second term will be smaller since r is in the denominator, and therefore there will be a less normal force felt by the passengers.